9 Inferenz für nominale Daten
In diesem Kapitel lernen wir, wie Häufigkeiten von qualitativ-nominalen Variablen statistisch verglichen werden. Für die Analyse qualitativer Daten existieren zahlreiche statistische Werkzeuge, von denen hier nur eine kleine Auswahl behandelt wird.
9.1 Lernziele
- Verwende einen \(\chi^2\)-Test, wenn die Unabhängigkeit von zwei nominalen Variablen geprüft werden soll:
- \(H_0\): Die zwei Variablen sind unabhängig.
- \(H_A\): Die zwei Variablen sind abhängig.
- Berechne die erwarteten Werte in Kreuztabellen als
\[E = \frac{Zeilensumme \times Spaltensumme}{Total}\]
- Berechne die Anzahl Freiheitsgrade der \(\chi^2\)-Verteilung als \(df = (Z-1)\times(S-1)\), wobei Z die Anzahl Zeilen und S die Anzahl Spalten darstellt.
9.2 Der \(\chi^2\)-Test
Der \(\chi^2\)-Test ist einer der ältesten Hypothesentests. Er wurde um 1900 von Karl Pearson entwickelt und später von Sir Ronald Fisher verfeinert. Der \(\chi^2\)-Test prüft, ob eine beobachtete Häufigkeitsverteilung einer nominalen Variable einer erwarteten Verteilung entspricht.
Beispiel: Hatten die Eltern von Kindern mit Allergien selber häufiger Allergien als die Eltern von Kindern ohne Allergien? Für diese Fragestellung wurde eine Zufallsstichprobe von 38 Kindern und deren Eltern zu ihrem Allergiestatus befragt. Codiert wurden die Daten mit 0 = keine Allergie und 1 = Allergie. (Holbreich et al. 2012)
9.2.1 Hypothesen und Signifikanzniveau
\(H_0\): Es besteht keine Beziehung zwischen einer Allergie bei Kindern und deren Eltern. Die relative Häufigkeit der Kinder, bei denen mindestens ein Elternteil eine Allergie hat(te), ist in den Populationen der Allergiker und der Nichtallergiker gleich. Wir nehmen also an: Die Wahrscheinlichkeit, dass mindestens ein Elternteil eine Allergie hatte, hat keinen Zusammenhang damit, ob das befragte Kind selber eine Allergie hat oder nicht.
\(H_A\): Es besteht eine Beziehung zwischen einer Allergie bei Kinderen und deren Eltern. Die relative Häufigkeit der Kinder, bei denen mindestens ein Elternteil eine Allergie hatte, unterscheidet sich zwischen den Populationen der Allergiker und der Nichtallergiker. Wir nehmen also an: Die Wahrscheinlichkeit, dass mindestens ein Elternteil eine Allergie hat(te), hängt davon ab, ob die befragte Person selber eine Allergie hat oder nicht.
Als Entscheidungsgrenze legen wir auch in diesem Fall ein Signifikanzniveau von \(\alpha = 0.05\) fest.
Für die Darstellung der Ergebnisse eignet sich eine Vierfeldertafel (Kreuztabelle, Kontingenztabelle):
##
## CONTINGENCY TABLES
##
## Contingency Tables
## --------------------------------------------------------------
## kind 0 1 Total
## --------------------------------------------------------------
## 0 Observed 17 5 22
## % of total 44.73684 13.15789 57.89474
##
## 1 Observed 7 9 16
## % of total 18.42105 23.68421 42.10526
##
## Total Observed 24 14 38
## % of total 63.15789 36.84211 100.00000
## --------------------------------------------------------------
##
##
## <U+03C7>² Tests
## --------------
## Value
## --------------
## N 38
## --------------- 17 (44.7%) Eltern, deren Kinder keine Allergie haben, sind keine Allergiker:innen.
- 7 (18.4%) Eltern, deren Kinder eine Allergie haben, sind keine Allergiker:innen.
- 5 (13.2%) Eltern, deren Kinder keine Allergie haben, sind Allergiker:innen.
- 14 (36.8%) Eltern, deren Kinder eine Allergie haben, sind Allergiker:innen.
Die Fälle, in denen Kinder und deren Eltern den gleichen Allergiestatus (beide Allergie oder beide keine Allergie) haben, machen zusammen über 78% der Fälle aus. Dies könnte ein Hinweis sein, dass eine Beziehung zwischen dem Allergiestatus von Kindern und deren Eltern besteht.
Als nächstes möchten wir erfahren, ob die beobachteten Daten den Erwartungen unter der Nullhypothese entsprechen. Dazu müssen wir die erwarteten Werte berechnen.
9.2.2 Berechnen der erwarteten Werte unter der Nullhypothese
Die Berechnung erfolgt am einfachsten, indem man die Zeilen- und Spaltensummen multipliziert und durch das Gesamttotal dividiert.
Schema:
| Spalte A | Spalte B | ||
|---|---|---|---|
| Zeile A | \(\frac{Zeilensumme A \times Spaltensumme A}{Total}\) | \(\frac{Zeilensumme A \times Spaltensumme B}{Total}\) | Zeilensumme A |
| Zeile B | \(\frac{Zeilensumme B \times Spaltensumme A}{Total}\) | \(\frac{Zeilensumme B \times Spaltensumme B}{Total}\) | Zeilensumme B |
| Spaltensumme A | Spaltensumme B | Total |
Übungshalber kann man das von Hand machen, einfacher geht es aber mit R/jamovi
##
## CONTINGENCY TABLES
##
## Contingency Tables
## ----------------------------------------------------------
## kind 0 1 Total
## ----------------------------------------------------------
## 0 Observed 17 5 22
## Expected 13.89474 8.105263 22.00000
##
## 1 Observed 7 9 16
## Expected 10.10526 5.894737 16.00000
##
## Total Observed 24 14 38
## Expected 24.00000 14.000000 38.00000
## ----------------------------------------------------------
##
##
## <U+03C7>² Tests
## --------------
## Value
## --------------
## N 38
## --------------Der Vergleich der erwarteten mit den beobachteten Werten unterstützt unsere bereits gemachte Vermutung: Die beobachteten Fälle, bei denen die Eltern den gleichen Allergiestatus haben wie die Kinder sind deutlich grösser, als wir sie unter der Nullhypothese erwarten würden.
9.2.3 Voraussetzungen
Um einen \(\chi^2\)-Test durchzuführen müssen folgende Voraussetzungen erfüllt sein:
- Die erwarteten Häufigkeiten in jeder Zelle der Tabelle müssen grösser als 5 sein. Ist diese Bedingung nicht erfüllt, kann der Fisher’s exakter Test verwendet werden.
- Der Test darf nur auf absolute Häufigkeiten und niemals auf relative Häufigkeiten angewendet werden.
- Die Daten stammen aus einer Zufallsstichprobe.
Um eine Entscheidung zu treffen, ob die Beziehung statistisch signifikant ist müssen wir die Testgrösse \(\chi^2\) berechnen. Die Formel dazu ist:
\[\chi^2 = \sum_{i=1}^n \frac{(O_i - E_i)^2}{E_i}\]
Das sieht für manche beängstigend aus, aber wir machen das hier nur, um das Prinzip zu zeigen: \(O\) steht für beobachtete Werte, \(E\) für erwartete Werte. Jetzt setzen wir unsere Werte aus der Tabelle oben in die Formel ein:
\[\chi^2 = \frac{(17-13.9)^2}{13.9} + \frac{(5-8.1)^2}{8.1} + \frac{(7-10.1)^2}{10.1} + \frac{(9-5.9)^2}{5.9} \approx 4.46\]
Unsere Testgrösse ist \(\chi^2 = 4.46\). Wie für die bereits bekannten Testgrössen \(z\) und \(t\) existiert auch für \(\chi^2\) eine spezifische Wahrscheinlichkeitsverteilung, eben die \(\chi^2\)-Verteilung. Es würde zu weit führen, im Detail auf diese Verteilung einzugehen, deren Form wie wie bei der t-Verteilung nur durch die Anzahl Freiheitsgrade df definiert ist. Anhand von Tabellen oder mit R/jamoviist es möglich, die Wahrscheinlichkeit für unseren \(\chi^2\)-Wert zu berechnen. In R/jamovi erfolgt diese Berechnung mit der Funktion pchisq(). Die Freiheitsgrade in einer \(n \times m\)-Tabelle werden berechnet als \(df = (n - 1)\times(m-1)\), im vorliegenden Fall also: \(df = (2-1)\times(2-1) = 1\).
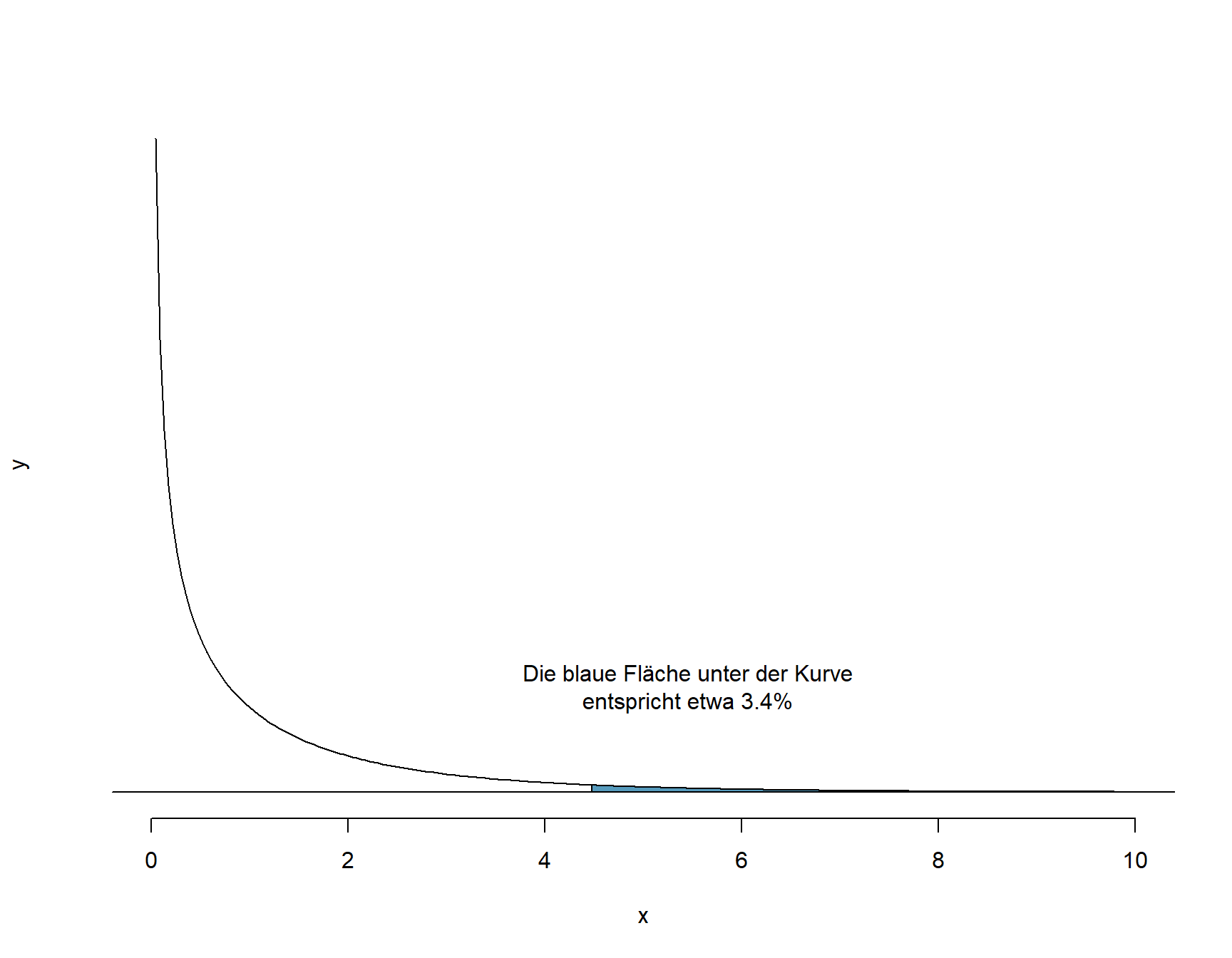
Abbildung 9.1: Chi-Quadrat-Verteilung für df = 1
Ohne komplizierte Berechnungen kann der Test in jamovidurchgeführt werden und ergibt:
##
## CONTINGENCY TABLES
##
## Contingency Tables
## ----------------------------------------------------------
## kind 0 1 Total
## ----------------------------------------------------------
## 0 Observed 17 5 22
## Expected 13.89474 8.105263 22.00000
##
## 1 Observed 7 9 16
## Expected 10.10526 5.894737 16.00000
##
## Total Observed 24 14 38
## Expected 24.00000 14.000000 38.00000
## ----------------------------------------------------------
##
##
## <U+03C7>² Tests
## -------------------------------------
## Value df p
## -------------------------------------
## <U+03C7>² 4.473688 1 0.0344206
## N 38
## -------------------------------------9.2.4 Interpretation des \(\chi^2\)-Tests
Die Wahrscheinlichkeit für \(\chi^2 = 4.47\) und \(df = 1\) ist \(p = 0.034\). Da der p-Wert kleiner als das Signifikanzniveau \(\alpha = 0.05\) ist, verwerfen wir die Nullhypothese zu Gunsten der Alternativhypothese.
Schlussfolgerung:
Untersucht wurde die Frage, ob eine Beziehung zwischen dem Allergiestatus von Kindern und dem Allergiestatus ihrer Eltern besteht. Anhand einer Zufallsstichprobe von 38 Kindern und deren Eltern konnte ein signifikanter Zusammenhang festgestellt werden: Kinder von Eltern ohne Allergien leiden eher seltener als erwartet an Allergien und Kinder von Eltern mit Allergien leiden eher häufiger als erwartet an Allergien, \(\chi^2(1)\) = 4.47, p = 0.034.
Hinweis: Bei einer Vierfeldertafel (2 Zeilen und 2 Kolonnen) ist der Zusammenhang zwischen der Zeilen- und der Kolonnenvariable statistisch signifikant auf dem Niveau von 5%, wenn der \(\chi^2\)-Wert grösser als 3.84 ist. Früher musste der exakte p-Wert in Tabellen der \(\chi^2\)-Verteilung nachgeschaut werden, heute macht das der PC.