5 Grundlagen der Inferenzstatistik

5.1 Einleitung

Here’s some shocking information for you - sample statistics are always wrong!

— Jim Frost

Deskriptive Statistik und Inferenzstatistik sind die zwei Hauptkategorien in der Statistik.

Deskriptive Statistik …

• dient der Beschreibung von Daten in einen Datensatz, der z.B. durch eine Zufallsstichprobe entstanden ist. Die Ergebnisse werden nicht verallgemeinert.
  
• berechnet Kennzahlen zu den Daten aus einem Datensatz und stellt die Daten grafisch dar; verwendet zur Beschreibung der Daten Kennzahlen wie Mittelwert, Median, Standardabweichung, Interquartilsabstand oder Korrelationskoeffizient.
  
• arbeitet nur mit den vorliegenden Daten im Datensatz; daher besteht keine Unsicherheit im Hinblick auf die Gültigkeit von Kennzahlen.

Inferenzstatistik …

• arbeitet mit Daten, die durch die Untersuchung einer Zufallsstichprobe aus einer grösseren Population ermittelt wurden. Ihre Aufgabe ist es, Rückschlüsse auf die Population zu ziehen, aus der diese Daten stammen. Die Ergebnisse der Stichprobe werden also auf eine grössere Gruppe oder Population übertragen.
  
• benötigt als Grundlage eine repräsentative Stichprobe aus der Population. Am besten gelingt das, indem die Beobachtungseinheiten für die Stichprobe zufällig aus der Population ausgewählt werden (Zufallsstichprobe).
  
• schätzt die wahren Kennzahlen in der Population auf Grundlage der Stichproben-Kennzahlen. Da Schätzungen immer mit einer gewissen Ungenauigkeit verbunden sind interessiert die Frage «Wie sicher können wir sein, dass der geschätzte Mittelwert \(\bar{x}\) dem wahren Populationsmittelwert \(\mu\) entspricht?».
  
• liefert Angaben, bis zu welchem Grad bzw. mit welcher Wahrscheinlichkeit wir unseren Schätzungen vertrauen können.

Die diesem Kapitel vorgestellten Grundlagen der Inferenzstatistik sind absolut essentiell für das Verständnis der nachfolgenden Themen. Es lohnt sich daher, für das Verständnis dieser Inhalte, genügend Zeit zu investieren.

5.2 Lernziele

1. Verwende eine Stichprobenkennzahl als Schätzung für einen Populationsparameter, z.B. wird der Stichprobenmittelwert verwendet um den Populationsmittelwert zu schätzen; beachte dass Punktschätzer und Stichprobenkennzahl synonym sind.

2. Beachte, dass Punktschätzer (wie z.B. der Stichprobenmittelwert) von Stichprobe zu Stichprobe variieren. Diese Variablilität wird als Stichprobenvariation bezeichnet. Ein Punktschätzer auf Grundlage einer Stichprobe, wird in der Nähe des Populationsparameters liegen, aber es ist sehr unwahrscheinlich, dass er diesen exakt trifft. Diese Abweichung wird als Stichprobenfehler bezeichnet.

3. Berechne die Stichprobenvariation des Mittelwerts, den Standardfehler SE mit der Formel (\(\sigma\) ist die Standardabweichung des Populationsparameters)

\[SE = \frac{\sigma}{\sqrt{n}}\]

• Wenn die Populationsstandardabweichung \(\sigma\) nicht bekannt ist, was meist der Fall ist, verwenden wir die Standardabweichung \(s\) der Stichprobe, um SE zu schätzen: \(SE = \frac{s}{\sqrt{n}}\).

4. Unterscheide zwischen Standardabweichung (\(s\) oder \(\sigma\)) und Standardfehler \(SE\): Die Standardabweichung misst die Variabilität in den Stichprobendaten, während der Standardfehler die Variabilität von Punktschätzern aus verschiedenen Stichproben der gleichen Grösse und aus der gleichen Population misst. Mit anderen Worten: Der Standardfehler ist ein Mass für die die Stichprobenvariation.

5. Erwarte, dass mit steigendem Stichprobenumfang die Stichprobenvariation abnimmt, da in der Formel zur Berechnung des Standardfehlers der Stichprobenumfang \(n\) im Nenner steht.

6. Intepretiere ein Konfidenzintervall (Vertrauensintervall, engl. confidence interval, Abk. \(CI\)) als glaubhaften Wertebereich für einen Populationsparameter.

7. Interpretiere das Konfidenzniveau (engl. confidence level) als den prozentualen Anteil von Zufallsstichproben, die Konfidenzintervalle ergeben, welche den wahren Populationsparameter enthalten.

8. Beachte, dass der zentrale Grenzwertsatz eine Aussage zur Verteilung von Punktschätzern erlaubt und dass diese Verteilung annähernd normal ist, wenn die Voraussetzungen erfüllt sind.

• Diese Voraussetzungen sind:

  • Annähernd Normalverteilung der Daten in der Population. Wenn die Verteilung in der Population unbekannt ist, kann diese Bedingung anhand eines Histogramms, eines Boxplots oder QQ-Plots überprüft werden.

  • Stichprobenumfang \(n\) > 30. Je grösser der Stichprobenumfang \(n\), desto unbedeutender wird die Verteilung, d.h. wenn \(n\) sehr gross ist, wird die Stichprobenverteilung nahezu normal sein, unabhängig von der Form der Verteilung in der Population.

  • Unabhängigkeit der Beobachtungseinheiten in einer Stichprobe: Die Unabhängigkeit der Beobachtungseinheiten kann sicher gestellt werden, indem diese zufällig ausgewählt werden (random sampling) und zufällig zu Gruppen zugeordnet werden (random assignment).

9. Merke, dass die Normalverteilung der Punktschätzer bedeutet, dass ein Konfidenzintervall berechnet werden kann:

\[Punktschätzer \pm z_{1-\frac{\alpha}{2}} \times SE\]

• \(z_{1-\frac{\alpha}{2}}\) entspricht den Grenzen der Standardnormalverteilung, innerhalb derer \(1-\alpha\) % der Daten liegen, \(1-\alpha\)% entspricht dem erwünschten Konfidenzniveau.

• Für einen Mittelwert ist dies: \(CI_{1-\alpha} = \bar{x} \pm z_{1-\frac{\alpha}{2}} \times SE\)

• Beachte, dass \(z_{1-\frac{\alpha}{2}}\) immer positiv ist!

11. Definiere bei der Berechnung des Konfidenzintervalls den Fehlerbereich (engl. margin of error, Abk. \(ME\)) als Abstand in beide Richtung vom Punktschätzer, d.h.

\[ME = z_{1-\frac{\alpha}{2}} \times SE\]

• \(ME\) entspricht genau einer Hälfte der Breite des Vertrauensintervalls.

12. Interpretiere ein Konfidenzintervall als “Wir können zu XX% darauf vertrauen, dass der wahre Populationsparameter innerhalb dieses Intervalls liegt” (XX% ist das gewünschte Vertrauensniveau).

• Beachte, dass die Interpretation immer im Kontext der Daten erfolgen sollte; erwähne immer, auf welche Population und welchen Parameter sich eine Aussage bezieht.

13. Erläutere, inwiefern das Prinzip von Hypothesentests mit dem Vorgehen am Gericht vergleichbar ist.

14. Denke daran, dass wir bei Hypothesentests immer zwei sich gegenseitig ausschliessende Aussagen untersuchen:

• Die Nullhypothese \(H_0\) steht für den skeptischen Standpunkt (kein Unterschied).
  
• Die Alternativhypothese \(H_A\) ist die Gegenhypothese zur Nullhypothese (es gibt einen Unterschied).

15. Beachte bei der Hypothesenbildung:

• Hypothesen beziehen sich immer auf Populationsparameter (z.B. Populationsmittelwert, \(\mu\)) und nicht auf die Stichprobenkennzahlen (z.B. Stichprobenmittelwert, \(\bar{x}\)). Es ist absurd, bezüglich der Stichprobenkennzahl eine Hypothese zu bilden, da diese ja aus der Stichprobe bekannt ist.

• Verstehe den Nullwert als den Wert eines Populationsparameters, welcher der Nullhypothese entspricht.

• Beachte, dass die Alternativhypothese \(H_A\) entweder einseitig (\(\mu\) > Nullwert oder \(\mu\) < Nullwert) oder zweiseitig formuliert werden kann (\(\mu \neq\) Nullwert). Die Wahl hängt von der konkreten Fragestellung ab. Wenn kein spezieller Grund für eine einseitige Alternativhypothese vorliegt, wähle und prüfe stets eine zweiseitige Alternativhypothese.

16. Um die Abweichung einer Stichprobe von der angenommenen Grundgesamtheit im Rahmen eines Hypothesentests zu messen, wird eine Teststatistik (engl.: test statistic) berechnet.

17. Definiere den \(p\)-Wert als die Wahrscheinlichkeit – unter der Bedingung, dass die Nullhypothese in Wirklichkeit gilt – den beobachteten Wert der Teststatistik oder einen in Richtung der Alternativhypothese extremeren Wert zu erhalten.

\[ p-Wert = P(beobachteter~oder~noch~extremerer~Wert~der~Prüfgrösse~|~H_0~wahr)\]

18. Berechne einen \(p\)-Wert als Fläche unter der Normalverteilungskurve (entweder auf eine Seite oder auf beide Seiten abhängig von der Alternativhypothese). Verwende zu diesem Zweck einen \(z\)-Wert oder einen \(t\)-Wert.

19. Verwerfe die Nullhypothese zugunsten der Alternativhypothese, wenn ein Konfidenzintervall den Nullwert nicht enthält.

20. Vergleiche den \(p\)-Wert mit dem Signifikanzniveau \(\alpha\) (typischerweise \(\alpha = 0.05\)), um zwischen den Hypothesen zu entscheiden:

• Verwerfe die Nullhypothese zugunsten der Alternativhypothese, wenn der \(p\)-Wert kleiner als das Signifikanzniveau ist, da dies bedeutet, dass es sehr unwahrscheinlich ist, eine mindestens so extreme Teststatistik rein durch Zufall zu erhalten. Interpretiere das Ergebnis in dem Sinn, dass die Daten Evidenz für die Alternativhypothese liefern.

• Verwerfe die Nullhypothese nicht, wenn der \(p\)-Wert grösser als das Signifikanzniveau ist, da dies bedeutet, dass es rein auf Zufall beruhen kann, eine mindestens so extreme Teststatistik zu erhalten. Interpretiere das Ergebnis so, dass die Daten keine Evidenz für die Alternativhypothese liefern.

• Merke: Fehlende Evidenz gegen die Nullhypothese bedeutet nicht, dass die Nullhypothese wahr ist. Die Nullhypothese kann nie angenommen oder bewiesen werden, da das Prinzip von Hypothesentests dies nicht erlaubt.

21. Denke daran, dass es immer möglich ist, einen Entscheidungsfehler zu begehen:

• Ein Fehler 1. Art bedeutet, dass die Nullhypothese verworfen wird, obwohl sie in Wirklichkeit wahr ist. Mit einem Signifikanzniveau von \(\alpha = 0.05\) nehmen wir in Kauf, dass dies bei einer von 20 Entscheidungen der Fall ist.

• Ein Fehler 2. Art bedeutet, dass wir die Nullhypothese nicht verwerfen, obwohl in Wirklichkeit die Alternativhypothese wahr ist. Damit verpassen wir die Erfassung eines Effektes, wo einer in Wahrheit vorhanden ist.

22. Beachte, dass die Wahrscheinlichkeit, einen Fehler 1. Art zu begehen dem Signifikanzniveau entspricht. Wähle das Signifkanzniveau so, dass es den Folgerisiken entspricht, die mit einem Fehler 1. oder 2. Art verbunden ist:

• Wähle ein kleineres \(\alpha\), wenn das Risiko einen Fehler 1. Art zu begehen, minimiert werden soll.
  
• Wähle ein grösseres \(\alpha\), wenn das Risiko einen Fehler 2. Art zu begehen, minimiert werden soll.

23. Definiere einen Effekt als Auswirkung oder als Folge einer Ursache. Wenn wir z.B. zwei Stichproben von Probanden mit und ohne Schlafmittel vergleichen und sich herausstellt, dass die Probanden mit dem Schlafmittel im Durchschnitt 1.5 Stunden länger schlafen, dann bezeichnen wir diese Differenz in der Schlafdauer zwischen den Gruppen als Effekt mit der Effektgrösse 1.5 Stunden.

24. Beachte, dass ein statistisch signifikanter Effekt nicht zwingend auch praktische Relevanz (Bedeutung) hat.

5.3 Grundbegriffe

5.3.1 Population

Im alltäglichen Sprachgebrauch besteht eine Population meist aus Menschen, z.B. die Einwohner:innen von Basel, Primarschüler:innen in einer Stadt oder Diabetiker:innen. In der Forschung können Populationen jedoch auch Objekte, Ereignisse, Firmen usw. sein. Zum Beispiel:

• Die Sterne der Milchstrasse
  
• Ein bestimmter Microchip für Handys
  
• Coronaviren SARS-CoV-2
• Hefekulturen in einer Brauerei

Je nach Fragestellung muss die Population sehr genau definiert werden, wenn man eine Studie durchführt. Dieser Aspekt wird im wissenschaftlichen Arbeiten bei der Behandlung der PICO-Fragestellung ausführlich besprochen.

Eine Subpopulation ist eine Untergruppe einer Population. So kann man die Population Bürger:innen der Schweiz in die Subpopulationen «Mann», «Frau» oder «höchster Schulabschluss» oder «sozialer Status» etc. oder Covid-19-Viren in die Subpopulationen Alpha (England), Beta (Südafrika), Gamma (Brasilien) und Delta (Indien) oder Omikron unterteilen. Die Einteilung in Subpopulationen ist v.a. dann von Bedeutung, wenn zwischen den Untergruppen systematische Unterschiede bestehen, wie das z.B. bei der Körpergrösse von Männern und Frauen der Fall ist (Abb. 5.1).

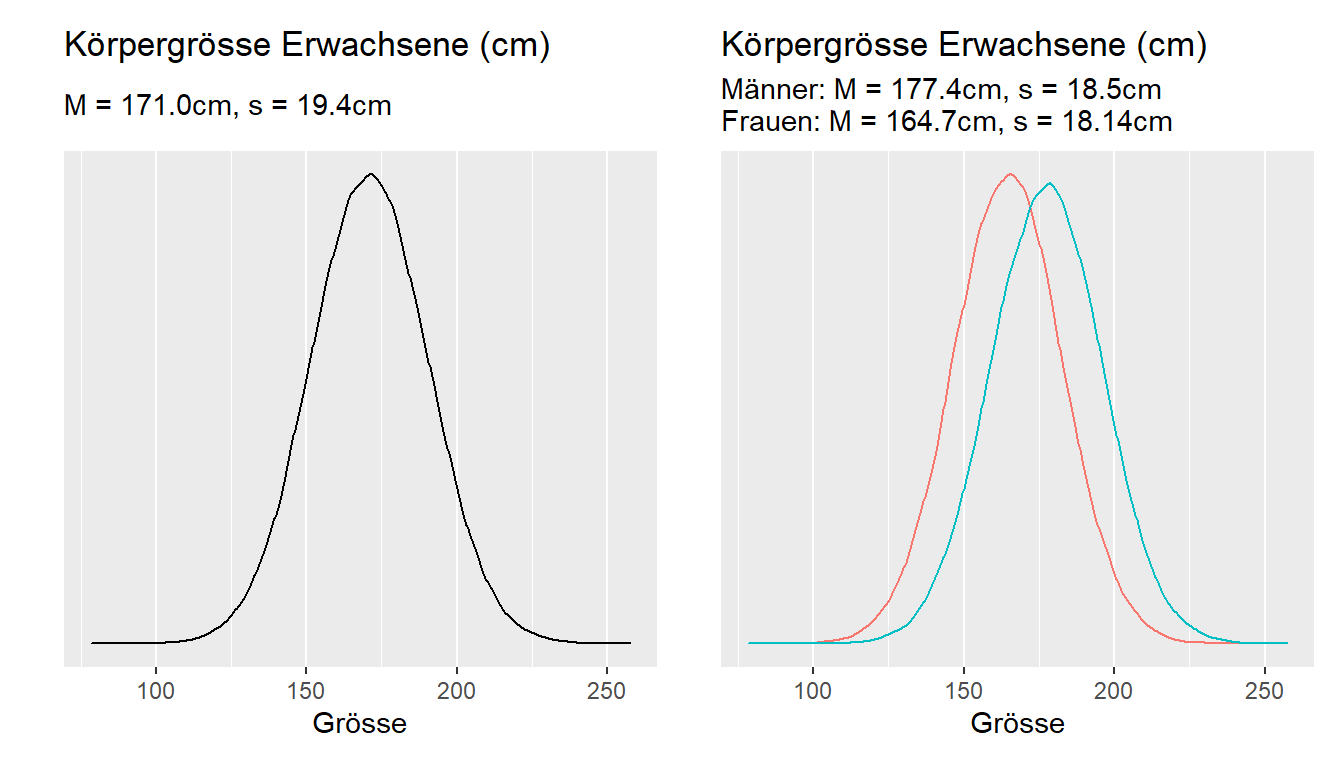
Abbildung 5.1: Körpergrösse einmal gemeinsam, einmal nach Geschlecht getrennt

5.3.2 Populationsparameter vs. Stichprobenkennzahl

Ein Parameter ist eine Kennzahl, die ein Merkmal einer ganzen Population beschreibt, z.B. ein Populationsmittelwert. Da es in der Regel nicht möglich ist, alle Beobachtungseinheiten einer Population zu messen, kennen wir Populationsparameter meist nicht. Obwohl wir Populationsparameter nicht messen können, existieren sie. Z.B. die durchschnittliche Körpergrösse aller Frauen in der Schweiz ist ein exakter Parameter, nur kennen wir diesen einfach nicht!

Populationsparameter werden mit griechischen Buchstaben, Stichprobenkennzahlen mit lateinischen Buchstaben gekennzeichnet (Ausnahmen bestätigen die Regel).

Mass	Populationsparameter	Stichprobenkennzahl
Umfang	\(N\)	\(n\)
Mittelwert	\(\mu\)	\(\bar{x}\)
Standardabweichung	\(\sigma\)	\(s\)
Korrelation	\(\rho\)	\(r\)

In der Inferenzstatistik dient die Stichprobenkennzahl dazu, den Populationsparameter zu schätzen. Folgende Schätzer (engl. estimate) für Populationsparameter kommen zum Einsatz:

• Punktschätzer verwenden eine Stichprobenkennzahl als besten Schätzer für einen Populationsparameter. Z.B. ist der Stichprobenmittelwert der beste Schätzer für den Populationsmittelwert. Wegen dem Stichprobenfehler sind leider Punktschätzer immer ungenau und die Grösse der Abweichung vom wahren Wert bleibt unbekannt.

• Intervallschätzer umfassen einen Wertebereich, der mit einer gewissen Wahrscheinlichkeit den Populationsparameter enthält. Solche Wertebereiche beinhalten eine Fehlergrenze (Fehlerbereich, engl. margin of error, Abk. \(ME\)) und berücksichtigen auf diese Weise die Ungenauigkeit eines Punktschätzers. Wenn wir statistische Resultate lesen, sollten wir uns immer fragen, wie gross diese Ungenauigkeit ist. Leider wird in den Medien dieser Fehlerbereich sehr oft nicht angegeben, wodurch eine falsche Genauigkeit suggeriert wird, die fakisch gar nicht vorhanden ist.

5.4 Methoden der Inferenzstatistik

In diesem Kurs lernen wir drei Methoden der Inferenzstatistik kennen:

• Hypothesentests, Signifikanztests verwenden Stichprobendaten um Fragen zu Punktschätzern zu beantworten. Z.B. ist der Populationsparameter grösser oder kleiner als ein bestimmter Wert oder unterscheiden sich die Parameter von zwei Populationen voneinander (Bsp. klinische Studie mit Interventions- und Kontrollgruppe).

• Konfidenzintervalle (engl. confidence intervalls, Abk. \(CI\)) dienen der Bestimmung von Populationsparametern und berücksichtigen die Unsicherheit (Ungenauigkeit) als Folge des Stichprobenfehlers. Sie geben einen Wertebereich an, in den der wahre Parameter mit einer gewissen Wahrscheinlichkeit fällt. Z.B. Ein 95%-Konfidenzintervall [176; 186] gibt an, dass wir zu 95% darauf vertrauen können, dass der wahre Populationsparameter innerhalb dieses Intervalls liegt.

• Korrelations- und Regressionsanalysen beschreiben den Zusammenhang zwischen einer oder mehreren unabhängigen Variablen und einer abhängigen Variablen. Auch diese Analyse umfasst Hypothesentests, welche die Entscheidung ermöglichen, ob ein Zusammenhang zwischen zwei oder mehr Variablen in einer Stichprobe effektiv auch in der Population besteht.

5.5 Stichprobenumfang und Fehlergrenze

Inferenzstatistik ist ein mächtiges Werkzeug, das uns erlaubt, aus relativ kleinen Stichproben etwas über eine ganze Population zu erfahren. Leider ist es jedoch so, dass auch wenn eine Studie akribisch genau durchgeführt wird, die Ergebnisse immer etwas falsch sein werden (bezogen auf die wahren Populationsparameter). Weil eine Stichprobe eben nicht die gesamte Population ist, können Stichprobendaten nie zu 100% präzis sein.

Das primäre Ziel der Inferenzstatistik ist es, von einer Stichprobe auf die Population zu verallgemeinern. Grosse Stichproben repräsentieren die Vielfalt einer Population besser als kleine Stichproben. Wenn wir zum Beispiel eine Studie zum Intelligenzquotienten durchführen und wir haben nur fünf Probanden zum testen, dann wird ein aussergewöhnlich hoher oder tiefer Wert den Stichprobenmittelwert erheblich beeinflussen. Wenn wir 50 Probanden untersuchen können, haben einzelne Extremwerte einen viel geringeren Einfluss.

5.5.1 Verteilung von Stichprobenkennzahlen

(Stichprobenverteilungen, engl. sampling distributions)

Für das Verständnis der Denkweise in der Statistik ist es ausserordentlich wichtig, sich vor Augen zu halten, dass wenn wir eine Zufallsstichprobe aus einer Population ziehen, diese Stichprobe nur eine von einer grossen Zahl möglicher Stichproben ist.

Zur Verdeutlichung führen wir ein simuliertes Experiment durch: Wir wissen, dass der IQ normalverteilt ist und dass der Populationsmittelwert des IQ-Scores bei \(\mu = 100\) und die Standardabweichung bei \(\sigma = 15\) liegt. Jetzt ziehen wir je 1000 Stichproben aus der Population im Umfang \(n = 5\), \(n = 25\), \(n = 100\) und stellen die ermittelten Stichprobenmittelwerte als Histogram dar.

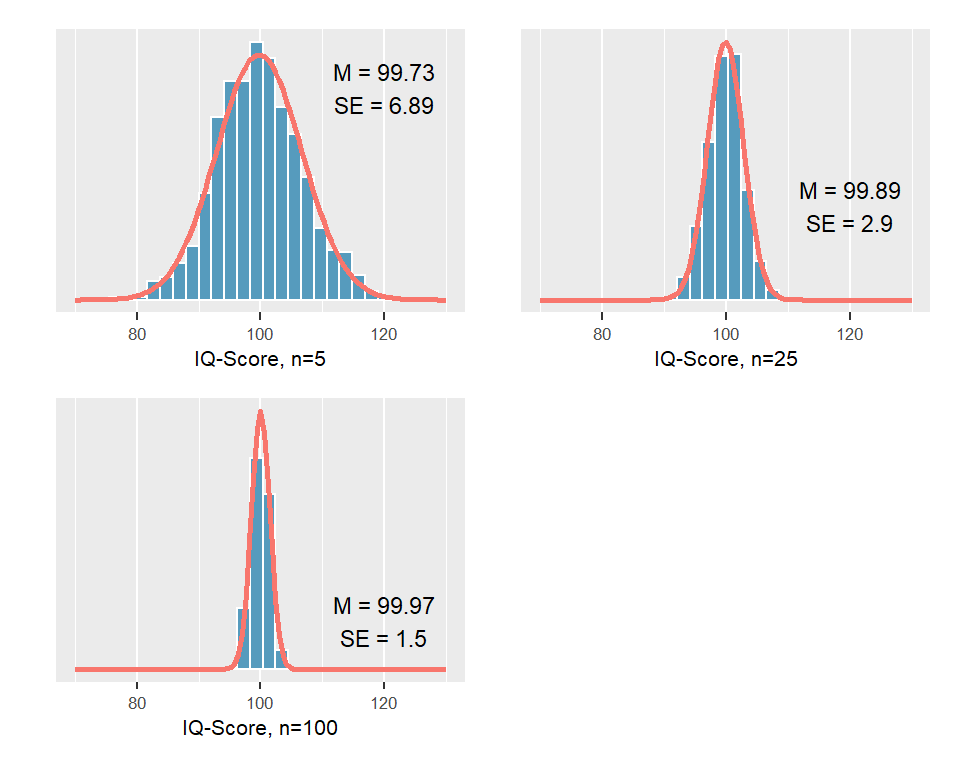
Abbildung 5.2: Stichprobenvariabilität für Mittelwerte von jeweils 1000 Stichproben

Was lernen wir aus diesem Experiment?

• Jeder Stichprobenmittelwert liegt in der Nähe des wahren Populationsmittelwertes, aber es ist wenig wahrscheinlich, dass ein Stichprobenmittelwert exakt den wahren Populationsmittelwert trifft.
  

• Je grösser die Stichprobe \(n\), desto näher liegen die geschätzten Mittelwerte beim wahren Populationsmittelwert. Mit anderen Worten: Je grösser der Stichprobenumfang \(n\), desto mehr können wir dem Stichprobenmittelwert vertrauen, dass er den wahren Populationsparameter repräsentiert.

• Die Variabilität dieser Verteilungen \(SE\) entspricht dem Stichprobenfehler in Abhängigkeit vom Stichprobenumfang \(n\). Grössere Stichprobenumfänge weisen einen kleineren Fehlerbereich auf.

• Die Stichprobenmittelwerte mehrerer Stichproben sind annähernd normalverteilt.

Was wir an unserem Beispiel nicht erkennen können ist, dass die Stichprobenverteilung der Mittelwerte selbst dann normalverteilt ist, wenn die zu Grunde liegende Verteilung der Populationsdaten nicht normal ist.

Hinweis: Die Online-App Central Limit Theorem for Means ermöglicht es, interaktiv verschiedene Szenarios durchzuspielen.

Im Experiment zum IQ-Score wird eine Verteilung für die Mittelwerte mehrerer Stichproben erstellt. Eine solche Stichprobenverteilung zeigt die Verteilung von Stichprobenkennzahlen (hier von Mittelwerten) mehrerer gleich grosser Stichproben aus einer bestimmten Population. Wie weiter unten erläutert, kann mit Hilfe eines mathematischen Tricks solche Stichprobenverteilungen aus einer einzigen Stichprobe geschätzt werden. Diese Verfahren bilden die theoretische Grundlage für Hypothesentests und Konfidenzintervalle.

Tipp: Bunnies, Dragons and the Normal World

5.6 Standardfehler (engl. standard error, Abk. \(SE\))

Die einzelnen Stichprobenmittelwerte in unserem Experiment liegen mehr oder weniger in der Nähe des wahren Populationsmittelwerts. Die Streuung der einzelnen Werte einer Stichprobenverteilung kann mit Hilfe der Standardabweichung quantifiziert werden. Die Standardabweichung eines Stichprobenmittelwerts beschreibt, wie weit typischerweise eine bestimmte Kennzahl vom wahren Populationsparameter entfernt ist oder mit anderen Worten, den Fehler dieser Schätzung. Die Standardabweichung einer Punktschätzung wird als Standardfehler bezeichnet. Der Standardfehler ist ein Mass für die Ungenauigkeit, die auf Grund der Stichprobenvariation mit unserer Punktschätzung verbunden ist.

Was genau ist jetzt aber der Unterschied zwischen Standardabweichung und Standardfehler? Sowohl der Standardfehler als auch die Standardabweichung befassen sich mit dem Mittelwert einer Stichprobe, das ist das Gemeinsame, aber …

• … der Standardfehler gibt Auskunft über die mittlere Abweichung des Mittelwerts einer Stichprobe vom tatsächlichen Mittelwert der Population; er beschreibt also die Beziehung zwischen Stichprobenkennzahl und Populationsparameter!

• … die Standardabweichung gibt uns Auskunft darüber, wie sehr die einzelnen Werte der Stichprobe um ihren Mittelwert streuen.

Üblicherweise steht, v.a. aus ökonomischen Gründen, nur eine einzige Stichprobe zur Verfügung und es ist auf den ersten Blick nicht offensichtlich, wie der Standardfehler \(SE\) aus einer einzigen Stichprobe berechnet werden kann. Wenn wir uns noch einmal den drei Experimenten oben zuwenden, stellen wir fest, dass \(SE\) mit zunehmendem Stichprobenumfang kleiner wird: \(SE\) = 6.89 bei n = 5, \(SE\) = 2.9 bei n = 25 und \(SE\) = 1.94 bei n = 100.

Es besteht demnach eine Beziehung zwischen der Grösse des Standardfehlers SE und dem Stichprobenumfang \(n\). Bei einem Stichprobenumfang \(n\) aus einer Population mit der Standardabweichung \(\sigma\), ist der Standardfehler des Stichprobenmittelwerts gleich

\[SE = \frac{\sigma}{\sqrt{n}}\]

Da die Standardabweichung einer Population üblicherweise unbekannt ist, wird sie mit der Standardabweichung der vorhandenen Stichprobe geschätzt: Anstelle von \(\sigma\) setzen wir \(s\) als Punktschätzer für \(\sigma\) ein:

\[SE = \frac{s}{\sqrt{n}}\]

5.6.1 Das Wurzel-n-Gesetz

Der Formel für die Berechnung des Standardfehlers \(SE\) ist zu entnehmen, dass sich dieser umgkehrt proportional zur Quadratwurzel des Stichprobenumfangs \(n\) verändert. Um also den Standardfehler beispielsweise zu halbieren, müsste daher den Stichprobenumfang vervierfacht werden.

s	n	SE
16	16	4
16	64	2

5.7 Konfidenzintervalle (auch Vertrauensintervalle, engl. confidence intervalls, Abk. \(CI\))

Die Kennzahl aus einer Stichprobe, z.B. der Mittelwert, liefert uns eine einzige Schätzung für einen Populationsparameter. Wie wir gesehen haben, sind solche Punktschätzungen eigentlich nie perfekt und wir würden gerne wissen, in welchem Mass wir auf diesen Wert vertrauen können, um unser Ergebnis korrekt interpretieren zu können. Hier kommen die Vertrauensintervalle ins Spiel. Es liegt eigentlich nahe, dass wir an Stelle einer Punktschätzung ein Werteintervall angeben können, in dem der wahre Populationsparameter mit grosser Wahrscheinlichkeit liegt. Das wäre dann zwar scheinbar weniger präzis, dafür etwas zuverlässiger (siehe unten Präzision versus Sicherheit).

Da ein Punktschätzer aus einer Stichprobe der überzeugendste Wert für einen gesuchten Populationsparameter ist, macht es Sinn, dass ein Konfidenzintervall um diese Schätzung herum konstruiert wird. Der Standardfehler, als Mass für die Ungenauigkeit des Punktschätzers, liefert die Angabe, wie breit das Konfidenzintervall konstruiert werden soll.

Der Standardfehler ist die Standardabweichung der Punktschätzung. Aus der 68-95-99.7-Regel wissen wir, dass ca. 95% der Daten innerhalb von zwei Standardabweichungen liegen. Damit können wir davon ausgehen, dass in ca. 95% der Fälle, der Punktschätzer innerhalb von plus/minus 2 Standardfehlern des Populationsparameters liegt. Wenn also die Breite eines Konfidenzintervalls plus/minus 2 Standardfehler zum Punktschätzer umfasst, dürfen wir zu 95% darauf vertrauen, dass dieses den wahren Populationsparameter enthält.

\[CI_{95} = Punktschätzung \pm 2 \times SE\]

Was bedeutet aber “zu 95% darauf vertrauen können”? Wenn viele Stichproben mit dem gleichen Stichprobenumfang aus einer Population gezogen werden und für jede Stichprobe das 95%-Konfidenzintervall bestimmt wird, dann werden im Durchschnitt 95% aller dieser Konfidenzintervalle den wahren Populationsparamter enthalten.

Kommen wir auf unser IQ-Score-Experiment zurück. Wir ziehen nochmals 25 Stichproben im Umfang \(n\) = 50 und konstruieren für jede Stichprobe das 95%-Konfidenzintervall für den IQ-Score.

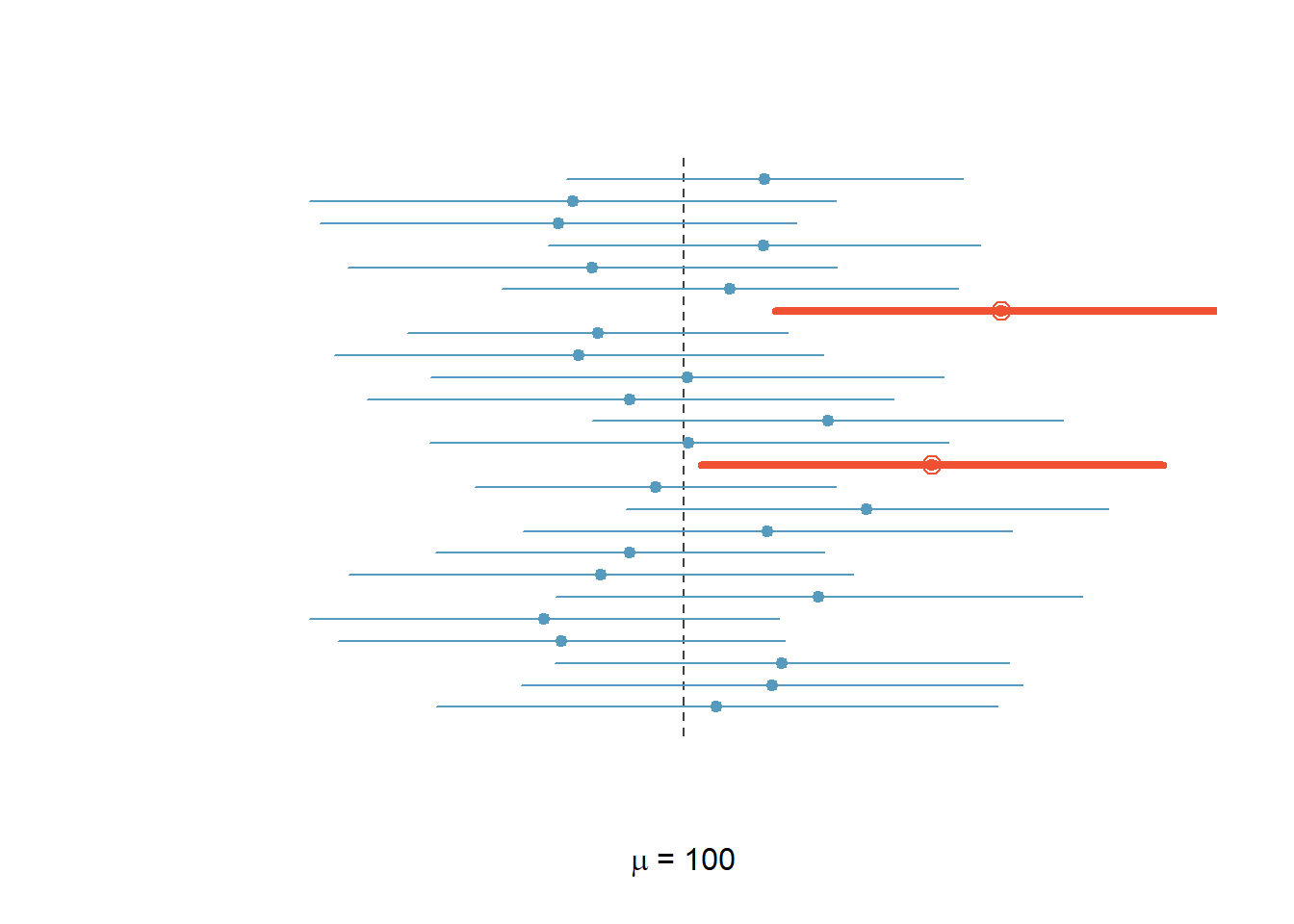
Abbildung 5.3: IQ-Score: 95%-Vertrauensintervalle für 25 Zufallsstichproben, \(n\) = 50

Von den 25 Stichproben enthalten in Abbildung 5.3 zwei (= 8%) den wahren Populationsmittelwert nicht. 8% ist etwas höher als erwartet. Allerdings ist zu berücksichtigen, dass wir das Experiment nur 25 Mal wiederholt haben. Mit weiteren Wiederholungen würde sich der Anteil, der 95%-Konfidenzintervalle, die den Populationsparameter nicht enthalten immer mehr bei 5% einpendeln Gesetz der grossen Zahlen.

Da der Standardfehler \(SE\) mit zunehmendem Stichprobenumfang \(n\) abnimmt, hat der Stichprobenumfang \(n\) einen grossen Einfluss auf die Breite von Konfidenzintervallen.

Tipp: Web-App Seeing Theory: Confidence Intervalls.

• Wähle \(Normal\) für Normalverteilung
  
• Stelle mit dem Regler das Konfidenzniveau \(1-\alpha\) = 0.95
  
• Beachte den Einfluss des Stichprobenumfangs auf die Breite der Konfidenzintervalle.
  
• Welchen Einfluss hat die Veränderung des Konfidenzniveaus \(1-\alpha\) auf die Breite der Konfidenzintervalle?

Erkenntnis:

• Je höher der Stichprobenumfang pro Stichprobe ist, desto schmaler werden die Konfidenzintervalle.
  
• Je höher das Konfidenzniveau wird, desto breiter werden die Konfidenzintervalle.

5.7.1 Anpassung des Konfidenzniveaus

Konfidenzintervalle haben eine untere und eine obere Grenze. In der Mitte steht die Stichprobenkennzahl als Schätzer für den Parameter, z.B. \(\bar{x}\). Die untere Grenze des Vertrauensintevalls wird berechnet als \(\bar{x} - Fehlerbereich ~ME\) und die obere Grenze \(\bar{x} + Fehlerbereich~ ME\).

\[ME = z \times SE\]

In der Formel zum 95%-Konfidenzintervall haben wir \(z = 2\) eingesetzt. Möglicherweise sind 95%-Vertrauensintervalle zu unsicher und man möchte eine grössere Zuverlässigkeit haben. In diesem Fall wird das Konfidenzniveau auf z.B. 99% erhöht. Es kann jedoch sein, dass keine so grosse Zuverlässigkeit erforderlich ist, dann kann das Konfidenzniveau auf z.B. 90% gesenkt werden. Das gewünschte Konfidenzniveau hat einen Einfluss auf den Fehlerbereich ME, der toleriert wird und somit auf den Faktor, mit dem der Standardfehler multipliziert werden muss. Allgemein formuliert:

\[CI_{1-\alpha} =\bar{x} \pm z_{1-\frac{\alpha}{2}} \times SE\]

Das \(z\) erinnert an die \(z\)-Werte der Standardverteilung und effektiv ist es das auch. Aus der 68-95-99.7-Regel wissen wir, dass wenn wir für \(z\) = 1 einsetzen ca. 68%, wenn wir für \(z\) = 2 einsetzen ca. 95% und für \(z\) = 3 ca. 99.7% der Daten enthalten sind. Üblich sind Konfidenzintervalle von 90%, 95% und 99%.

\(\alpha/2\)	Konfidenzniveau \(1-\alpha\)	\(z_{1-\frac{\alpha}{2}}\)
.05	.9 = 90%	1.645
.025	.95 = 95%	1.96
.005	.99 = 99%	2.58

Anmerkungen:

• Eine Erklärung zur Bedeutung des Signifikanzniveaus \(\alpha\) folgt weiter unten. Man kann hier schon ahnen, dass \(\alpha\) etwas mit dem Fehler zu tun hat, den wir bereit sind, in Kauf zu nehmen.
  
• Zur Schätzung des 95%-Bereichs kann in der Praxis der Faktor 2 verwendet werden, genauer ist aber 1.96.

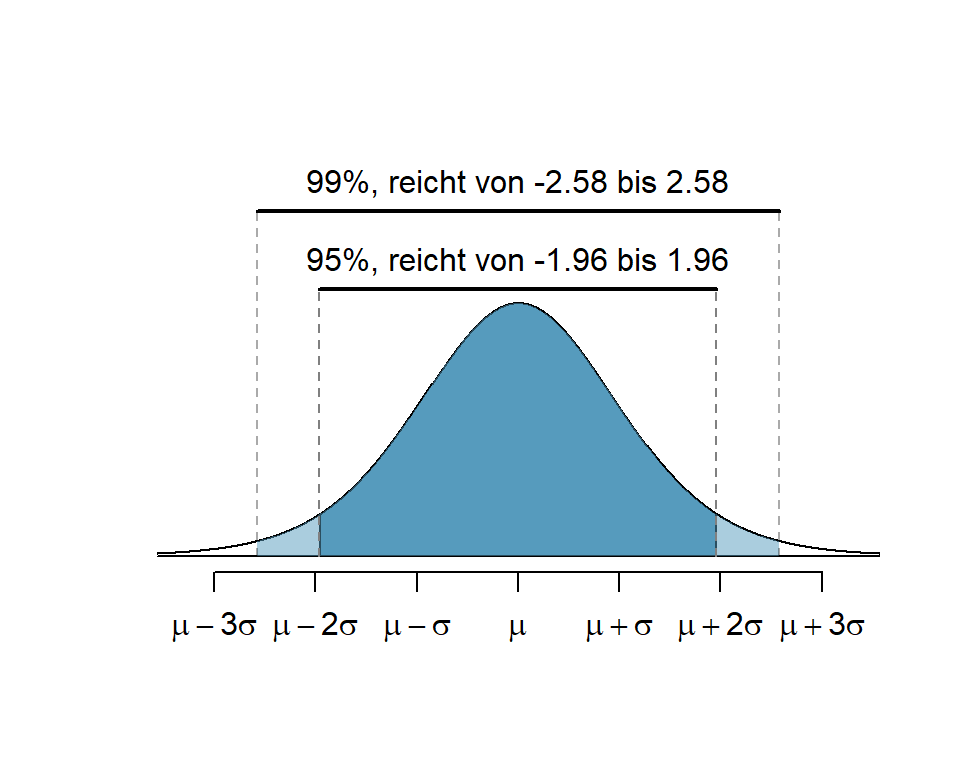
Abbildung 5.4: Flächen für 95%-CI und 99%-CI

Die Abbildung 5.4 zeigt, dass mit grösserem \(z\) die Fläche zwischen \(-z\) und \(+z\) grösser wird. Für das 99% Konfidenzintervall wurde \(z\) so gewählt, dass 99% der Fläche unter der Kurve zwischen \(-z\) und \(+z\) liegt. Es ist logisch, dass, je sicherer wir sein wollen, dass das Konfidenzintervall den wahren Parameter enthält, desto breiter muss es sein.

5.7.2 Präzision versus Sicherheit

Es besteht ein direkter Zusammenhang zwischen der Genauigkeit eines Konfidenzintervalls und seiner Zuverlässigkeit. Schmale Konfidenzintervalle bedeuten hohe Präzision. Wenn wir die Formel zur Berechnung von Konfidenzintervallen betrachten, erkennen wir, dass drei Variablen die Grösse des Fehlerbereichs ME bestimmen:

• die Standardabweichung \(s\) der Stichprobenkennzahl: je grösser \(s\), desto breiter das Konfidenzintervall.

• der Stichprobenumfang \(n\): je grösser \(n\), desto kleiner ist das Konfidenzintervall.

• die Wahl von \(z\): die Wahl eines kleineren \(z\)-Werts ergibt ein kleineres Konfidenzintervall als die Wahl eines grösseren \(z\)-Werts. Allerdings ist das Konfidenzniveau bei einem kleineren \(z\)-Wert auch geringer als bei einem grösseren \(z\)-Wert. Wählen wir z.B. einen \(z\)-Wert von 1.645 können wir nur zu 90% darauf vertrauen, dass der wahre Populationsparameter im Konfidenzintervall liegt. Wählen wir jedoch \(z\) = 1.96, wird zwar der Fehlerbereich grösser (weniger Präzision), dafür steigt das Konfidenzniveau auf 95% (mehr Zuverlässigkeit).

5.7.3 Voraussetzungen

Wichtige Voraussetzungen dafür, dass die Stichprobenverteilung von \(\bar{x}\) annähernd normalverteilt ist und dass die Schätzung für den Standardfehler \(SE\) genügend genau ist, sind:

• Die einzelnen Beobachtungseinheiten der Stichprobe sind unabhängig voneinander.

• Der Stichprobenumfang ist gross: \(n > 30\) ist eine gute Faustregel

• Die Populationsdaten sind nicht allzu stark schief verteilt. Die Beurteilung dieser Bedingung ist im Einzelfall nicht immer ganz einfach.

Wie kann man sicher sein, dass die Beobachtungseinheiten in der Stichprobe voneinander unabhängig sind?

• Wenn die Beobachtungseinheiten aus einer Zufallsstichprobe (randomisierte Zuteilung) stammen und weniger als 10% der Gesamtpopulation umfassen, dann dürfen wir annehmen, dass sie unabhängig sind.
  
• Beobachtungseinheiten in einer Studie gelten als unabhängig, wenn sie randomisiert den Gruppen (z.B. Interventions- und Kontrollgruppen) zugeteilt werden.

5.7.4 Interpretation von Konfidenzintervallen

Aufmerksamen Leser:innen mag aufgefallen sein, dass die sprachliche Formulierung von Konfidenzintervallen etwas holprig tönt:

Wir können zu XX% darauf vertrauen, dass der wahre Populationsparameter zwischen … und … liegt.

De facto bedeutet dies, dass wenn wir 100 Stichproben mit dem gleichen Stichprobenumfang aus einer Population ziehen, werden im Durchschnitt XX Stichproben den wahren Populationsparameter enthalten.

Bei der Formulierung von Konfidenzintervallen kommt es häufig zu zwei typischen Fehlern:

• Zu sagen, dass ein Konfidenzintervall mit einer Wahrscheinlichkeit von XX% den Populationsparameter enthält ist nicht korrekt. Das Konfidenzintervall enthält den Populationsparameter oder nicht, wir wissen es einfach nicht, aber wir können zu XX% darauf vertrauen. Das ist ein sehr subtiler sprachlicher Unterschied.

• Zu sagen, dass XX% der Populationsdaten in das Konfidenzintervall fallen, ist falsch. Das Konfidenzintervall bezieht sich ausschliesslich auf den gesuchten Populationsparameter und nicht auf die Populationsdaten!

5.8 Hypothesen in der Statistik

Wir beginnen mit der Frage, ob Studierende heute öfter ins Krafttrainig gehen als vor 10 Jahren. Es liegen uns Daten von Studien aus den Jahren 2010 und 2020 vor, welche u.a. die Frage bearbeitet haben “Wie oft pro Woche gehen Studierende ins Krafttraining”. Unsere Hypothesen könnten lauten:

• \(H_0:\) Die durchschnittliche Anzahl Krafttrainings der Studierenden ist in den Jahren 2010 und 2020 die gleiche. Es gibt keinen Unterschied in der durchschnittlichen Anzahl Krafttrainings pro Woche zwischen den Studierenden 2010 und 2020.

• \(H_A:\) Die durchschnittliche Anzahl Krafttrainings der Studierenden ist in den Jahren 2010 und 2020 nicht gleich. Es gibt einen Unterschied in der durchschnittlichen Anzahl Krafttrainings pro Woche zwischen den Studierenden 2010 und 2020.

\(H_0\) bezeichnen wir als Nullhypothese, \(H_A\) als Alternativhypothese. In der Regel, steht die Nullhypothese für einen skeptisch-konservativen Standpunkt: Es gibt keinen Unterschied. Die Alternativhypothese ist dagegen der Standpunkt der eine neue Perspektive eröffnet und die Möglichkeit in Betracht zieht, dass ein Unterschied besteht.

Die wissenschaftliche Position ist grundsätzlich eine skeptische. Das bedeutet, dass die Nullhypothese \(H_0\) nicht verworfen wird, es sei dann es bestehe starke Evidenz für die Alternativhypothese \(H_A\). In diesem Fall wird \(H_0\) zu Gunsten von \(H_A\) verworfen.

Dieses Prinzip wird auch in der Rechtssprechung angewandt. Ein Angeklagter gilt so lange als unschuldig (\(H_0\) = Unschuldsvermutung), bis mit ausreichender Evidenz das Gegenteil (\(H_A\)) bewiesen ist. Auch wenn ein Angeklagter frei gesprochen wird (\(H_0\) wird nicht verworfen) ist es möglich, dass er schuldig ist, aber die Beweislage war in diesem Fall ungenügend. Daher gilt

Auch wenn wir die Nullhypothese nicht verwerfen können, heisst das nicht, dass wir sie als wahr akzeptieren.

Keine starke Evidenz für die Alternativhypothese zu finden bedeutet daher nicht, dass wir die Nullhypothese akzeptieren.

5.8.1 Mathematische Formulierung von Hypothesen

Damit Hypothesen mit statistischen Methoden überprüft werden können, müssen sie zuerst mathematisch formuliert werden. Im Beispiel zur Trainingshäufigkeit von Studierenden haben wir die Null- und die Alternativhypothese bereits sprachlich formuliert und können sie jetzt im Hinblick auf die statistische Auswertung mathematisch formulieren:

Nullhypothese:

\(H_0: \mu_{Training2020}=\mu_{Training2010}\) bzw.
\(H_0: \mu_{Training2020}-\mu_{Training2010} = 0\)

Alternativhypothese:

\(H_A: \mu_{Training2020}\neq\mu_{Training2010}\) bzw.
\(H_A: \mu_{Training2020}-\mu_{Training2010} \neq 0\)

(In jeweils der Formulierung (\(=0,~\neq0\)) erkennen Sie, warum das Ganze Nullhypothese genannt wird)

Ein Fehler, der häufig bei der mathematischen Formulierung von \(H_0\) und \(H_A\) gemacht wird ist:

\(H_0: \bar{x}_1 = \bar{x}_2\)
\(H_A: \bar{x}_1 \neq \bar{x}_2\)

Warum ist das falsch? Weil bei der Formulierung der Hypothesen nicht für die Stichprobenmittelwerte interessieren, sondern die Populationsparameter! Für die Stichprobenmittelwerte brauchen wir ja keine Hypothesen, die sind bekannt: entweder unterscheiden sich die beiden Stichprobenkennzahlen identisch oder sie unterscheiden sich nicht.

In der Umgangssprache und in der medizinischen Diagnostik hat der Begriff Hypothese eine etwas andere Bedeutung: Wir verwenden ihn, wenn wir eine Vermutung oder eine Annahme über die Ursache eines Zustands oder Ereignisses haben. Aus der Perspektive der Statistik handelt es sich dabei typischerweise um eine Alternativhypothese. Im Unterschied zu Hypothesen im Alltag muss eine Hypothese in der Wissenschaft prüfbar, d.h. falsifizierbar sein. In der statistischen Praxis empfiehlt es sich daher, die Null- und Alternativhypothese immer mathematisch zu formulieren.

5.8.2 Hypothesen mittels Konfidenzintervallen prüfen

Betrachten wir die Ergebnisse der Studien aus den Jahren 2010 und 2020. An wie vielen Tagen haben die Studierenden in den beiden Stichproben (n = 92) pro Woche durchschnittlich trainiert?

Tabelle 5.1: Mittelwert (M) und Standardabweichung (s) für Anzahl Trainingstage 2010 und 2020

name	n	M	s
training_2010	92	3.01	2.46
training_2020	92	2.79	2.60

2010 haben die Studierenden durchschnittlich an 3.01 Tagen und 2020 an 2.79 Tagen trainiert. Es sieht demnach so aus, dass die Studierenden 2020 im Durchschnitt etwas seltener ins Training gingen, als die Studierenden in 2010.

\(H_0: \mu_{2020} = \mu_{2010}\)
\(H_A: \mu_{2020} \neq \mu_{2010}\)

Der Mittelwert aus 2010 ist in dieser Fragestellung Nullwert (Die Nullhypothese ist gültig wenn \(\mu_{2020} - \mu_{2010 = 0}\))

\(H_0: \mu_{2020} = 3.01\)
\(H_A: \mu_{2020} \neq 3.01\)

Die Berechnung des 95%-Konfidenzintervalls für den Mittelwert aus 2020 ergibt:

\(CI_{95} = \bar{x} \pm 1.96 \times \frac{s}{\sqrt{n}}\)

\(CI_{95} = 2.79 \pm 1.96 \times \frac{2.6}{\sqrt{92}}\)

### R-Code

nullvalue <- 3.01
m <- 2.79
s <- 2.6
n <- 92
SE <- s/sqrt(n)
z <- 1.96
ME <- z * SE

# 95%-CI berechnen
ci <- m + c(-1, 1) * ME

# 95%-CI auf zwei Nachkommastellen runden und ausgeben
ci <- round(ci, 2)
print(paste("95%-CI [", ci[1], "; ", ci[2], "]", sep = ""))

## [1] "95%-CI [2.26; 3.32]"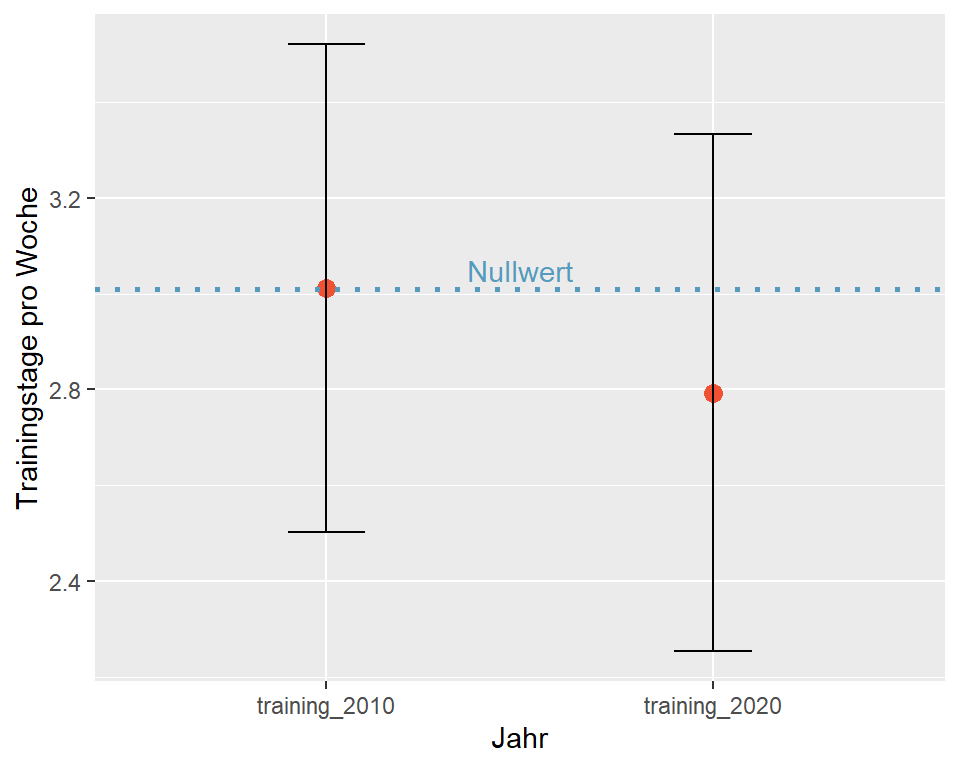

Abbildung 5.5: 95%-CI für Trainingstage pro Woche

Intepretation: Das 95%-Konfidenzintervall für den Stichprobenmittelwert 2020 ist [2.26; 3.32]. Wir können zu 95% darauf vertrauen, dass die durchschnittliche Anzahl Trainings, welche die Studierenden von 2020 besuchten zwischen 2.26 und 3.32 lag. Dieses Vertrauensintervall beinhaltet den Mittelwert aus der Stichprobe von 2010 (Nullwert). Das heisst, dieser Wert ist auch für die Studierenden von 2020 durchaus plausibel. Es liegt daher keine Evidenz dafür vor, dass \(H_0\) verworfen werden kann.

Merke: Wenn ein Konfidenzintervall den Nullwert beinhaltet, liegt keine ausreichende Evidenz dafür vor, dass \(H_0\) verworfen werden kann.

5.8.3 Entscheidungsfehler

Kommen wir noch einmal zurück zum Beispiel am Gericht: Die Aufgabe des Gerichts ist es, ein Urteil über den Angeklagten zu fällen. Auf Grund der Unschuldsvermutung gilt:

\(H_0:\) Der Angeklagte ist unschuldig.
\(H_A:\) Der Angeklagte ist schuldig.

Die Anklage wird im Laufe des Verfahrens Hinweise auf die Schuld des Angeklagten präsentieren. Sein Verteidiger wird entlastende Argumente vorbringen. Irgendwann kommt dieses Argument- und Gegenargument-Spiel zu Ende und das Gericht muss ein Urteil fällen. Da in vielen Fällen die Fakten nicht ganz eindeutig sind (man nennt das juristisch einen Indizienfall), besteht die Möglichkeit, dass das Gericht zu einem Fehlurteil kommt. Vier verschiedene Urteile sind möglich:

	H0 nicht verwerfen	H0 zugunsten HA verwerfen
H0 ist wahr	okay	Fehler 1. Art
HA ist wahr	Fehler 2. Art	okay

Ist der Angeklagte in Wahrheit …

• unschuldig und wird vom Gericht freigesprochen, ist das Urteil korrekt.
  
• schuldig und wird vom Gericht verurteilt, ist das Urteil korrekt.
  
• unschuldig, wird aber vom Gericht verurteilt, ist das ein Fehlurteil (Fehler 1. Art).
  
• schuldig, wird aber vom Gericht freigesprochen, ist das ein Fehlurteil (Fehler 2. Art).

Wie im Gericht müssen in der Statistik Entscheide getroffen werden, auch wenn die Datenlage meist nicht eindeutig ist. Unser Wissen ist immer unsicher, weil wir nie alle Daten haben, und es ist, wie am Gericht, nahezu unvermeidbar, dass wir Fehlentscheide treffen.

• Fehler 1. Art, \(\alpha\)-Fehler: \(H_0\) wird zugunsten \(H_A\) verworfen, obwohl \(H_0\) wahr ist. Es besteht vermutlich Einigkeit darüber, dass dies ein schwerwiegender Fehler ist. Er bedeutet am Gericht, dass ein Unschuldiger eine Strafe verbüssen muss. In der Medizin kann das bedeuten, dass eine teure Therapie, die in Wirklichkeit völlig nutzlos ist, eine Zulassung erhält und die Gesundheitskosten belastet.
  
• Fehler 2. Art, \(\beta\)-Fehler: \(H_0\) wird nicht verworfen, obwohl \(H_A\) wahr ist. Auch dieser Fehlerentscheid ist unschön, aber wir stimmen Sir William Blackstone vermutlich zu, dass er weniger schwerwiegende Folgen hat, als ein Fehler 1. Art.

5.8.4 Signifkanzniveau

Jeder Entscheid birgt das Risiko eines Fehlentscheids. Bei der Erläuterung der Hypothesentests haben wir etwas schwammig formuliert, dass \(H_0\) verworfen wird, wenn starke Evidenz für \(H_A\) vorliegt. Was aber bedeutet stark? Als Faustregel gilt, dass wir bereit sind, in nicht mehr als 5% der Fälle, bei denen \(H_0\) effektiv wahr ist, die Nullhypothese fälschlicherweise zurückzuweisen. Oder anders formuliert: Wir erlauben uns einen Fehler 1. Art bei 5% der Entscheidungen bezüglich \(H_0\). Diese (willkürlich) festgelegte Grenze wird als Signifikanzniveau bezeichnet. Oft wird das Signifikanzniveau mit dem griechischen Buchstaben \(\alpha\) angegeben und wir schreiben: \(\alpha = 0.05\).

Das Signifikanzniveau, gibt an, wie hoch das Risiko ist, das man bereit ist einzugehen, einen Fehler 1. Art zu begehen.

In den meisten Studien im Gesundheitsbereich wird ein Wert für \(\alpha=0.05\) verwendet. Diese Entscheidungsgrenze bei der Entwicklung der Studienmethodik festgelegt und ist gewissermassen willkürlich. Je nach Fragestellung kann auch \(\alpha=0.1\) oder \(\alpha=0.01\) festgelegt werden.

Wenn wir bei einem Hypothesentest, bei dem \(H_0\) wahr ist, ein 95%-Konfidenzintervall verwenden, können wir einen Entscheidungsfehler begehen, wenn ein Punktschätzer > 1.96 Standardabweichungen vom Mittelwert entfernt ist. Bei \(\alpha=0.05\) passiert uns das in ca. 5% der Fälle (2.5% auf beiden Seiten der Kurve).

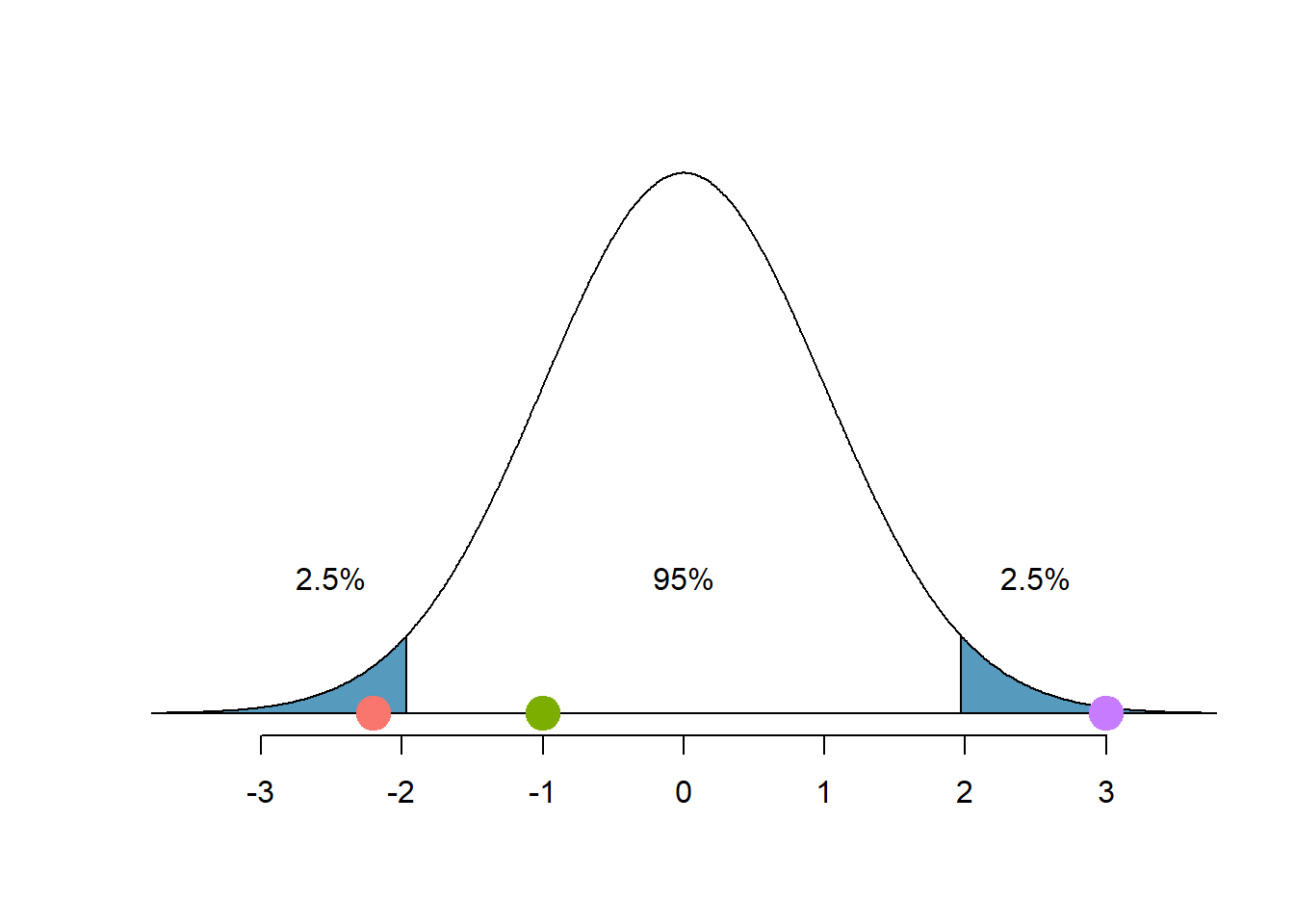
Abbildung 5.6: Nullhypothese: 5%-Verwerfungsbereich & 95% Annahmebereich

Die Kurve in Abbildung 5.6 zeigt die Verteilung der Daten unter \(H_0\) und \(H_0\) ist in diesem Beispiel effektiv wahr. Die beiden blauen Flächen am Ende der Kurve ergeben zusammen einen Verwerfungsbereich für \(H_0\) von 5%. Der Annahmebereich beträgt 95%. Liegt der Punktschätzer im Verwerfungsbereich (roter Punkt \(z\) = -2.2, violetter Punkt \(z\) = +3), verwerfen wir die \(H_0\) und begehen einen Fehler 1. Art. Liegt der Punktschätzer im Annahmebereich (grüner Punkt) wird \(H_0\) nicht verworfen.

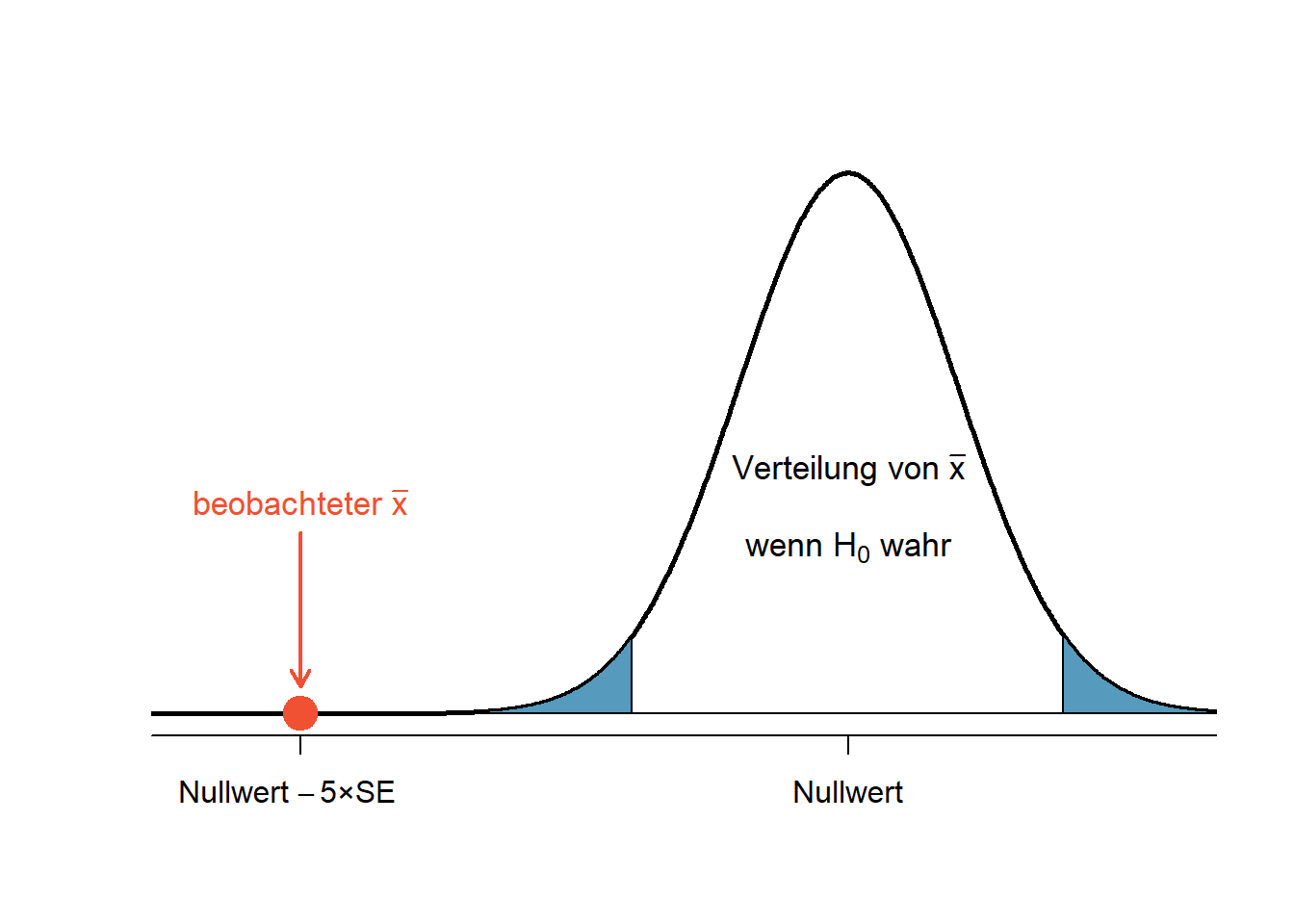
Abbildung 5.7: Starke Evidenz gegen die Nullhypothese

Im abgebildeten Fall (Abb. ?? liegt der Punktschätzer 5 Standardfehler vom Mittelwert der Verteilung unter der Nullhypothese entfernt. Dies bedeutet starke Evidenz gegen \(H_0\). Die Wahrscheinlichkeit ist gering, einen Fehler 1. Art zu begehen, wenn \(H_0\) in diesem Fall verworfen wird.

5.9 Der p-Wert

Der letzte Abschnitt schloss mit der Feststellung, dass wir starke Evidenz gegen die Nullhypothese haben. Aber wie stark ist stark? Hier kommt jetzt der \(p\)-Wert ins Spiel, dem wir in fast allen Studien begegnen.

Der p-Wert ist eine Möglichkeit, die Stärke der Evidenz gegen die \(H_0\) zugunsten der \(H_A\) zu quantifizieren. Formell betrachtet ist der \(p\)-Wert eine bedingte Wahrscheinlichkeit (p steht als Abkürzung für probability).

Der \(p\)-Wert gibt die Wahrscheinlichkeit für das Auftreten eines Ereignisses oder eines noch extremeren Ereignisses an, unter der Annahme, dass die Nullhypothese wahr ist.

Zu technisch? Dann vielleicht so: Wenn wir einen statistischen Test durchführen, können wir folgende Frage beantworten: “Wenn meine Intervention (ein Medikament, eine Behandlung etc.) absolut keinen Effekt hat (Nullhypothese), wie gross ist dann die Wahrscheinlichkeit für das Resultat, das meine Studiendaten ergeben haben?” Der \(p\)-Wert gibt diese Wahrscheinlichkeit an.

Nehmen wir das Beispiel aus der letzten Abbildung: Der beobachtete Stichprobenmittelwert \(\bar{x}\) liegt 5 Standardfehler vom Nullwert (Mittelwert der Verteilung unter der Nullhypothese) entfernt. Wie gross ist die Wahrscheinlichkeit, dass ein solches Ereignis eintritt, wenn die \(H_0\) wahr ist?

Minus 5 SE bedeutet \(z\) = -5. Leider ist es so, dass keine \(z\)-Tabelle so extreme \(z\)-Werte darstellt, weil solche Werte unter der Nullhypothese sehr unwahrscheinlich sind. Wir können aber mit einer einfachen Funktion in R die Frage beantworten:

### R-Code

# die Funktion pnorm(z-Wert) berechnet die Fläche der Normalverteilung 
# links vom z-Wert.
pnorm(-5) 

## [1] 2.866516e-07

Interpretation: Die Wahrscheinlichkeit für unser Ereignis ist p = 0.000000029, d.h. 0.0000029%. Zugegeben, das ist sehr unwahrscheinlich und wir können guten Gewissens \(H_0\) zugunsten der \(H_A\) verwerfen, insbesondere wenn wir \(\alpha=0.05\) als Entscheidungsgrenze definiert haben. Ist der p-Wert kleiner als unser Signifikanzniveau, spricht man in der Statistik von einem signifikanten Ergebnis. Man bringt damit zum Ausdruck, dass das Ergebnis nicht auf purem Zufall bzw. natürlicher Stichprobenvariation beruht, sondern dass ein echter Unterschied zwischen der Population der Nullhypothese (z.B. der Kontrollgruppe) und der beobachteten Population (z.B. der Interventionsgruppe) besteht.

Häufige Fehlinterpretationen des \(p\)-Werts: Der \(p\)-Wert ist nicht

• die Wahrscheinlichkeit, dass die Nullhypothese stimmt.
  
• die Wahrscheinlichkeit, dass die Alternativhypothese falsch ist.
  
• die Wahrscheinlichkeit, dass das Ergebnis nur durch Zufall entstanden ist.
  
• eine Quantifizierung der (klinischen) Relevanz der Ergebnisse.
  
• eine Quantifizierung der Stärke eines Effekts.

Zusammenfassung

• Die Nullhypothese ist Ausdruck einer skeptischen Position; sie geht davon aus, dass es keinen Unterschied gibt. Diese Position wird nur verworfen, wenn ausreichend Evidenz für die Alternativhypothese (= es gibt einen Unterschied) vorliegt.
  
• Ein kleiner \(p\)-Wert bedeutet, dass eine kleine Wahrscheinlichkeit für das Ergebnis einer Punktschätzung (oder noch ein extremeres Ergebnis) besteht, wenn die Nullhypothese wahr ist. Wir interpretieren das als starke Evidenz zugunsten der Alternativhypothese.
  
• Wir verwerfen die Nullhypothese, wenn der \(p\)-Wert kleiner als unser Signifikanzniveau \(\alpha\) (üblicherweise 0.05) ist. Andernfalls halten wir die Nullhypothese aufrecht.
  
• Wir formulieren die Schlussfolgerung eines Hypothesentests stets so, dass auch Nichtstatistiker:innen diese verstehen können.

5.9.1 Statistische Macht (Power)

Statistische Macht (auch Power, Trennschärfe) ist die Wahrscheinlichkeit, dass ein Effekt entdeckt wird, wenn der Effekt auch tatsächlich existiert.

Statistische Macht ist definiert als die Wahrscheinlichkeit, korrekterweise eine falsche Nullhypothese zurückzuweisen.

Wenn die statistische Power hoch ist, sinkt die Wahrscheinlichkeit, einen Typ-II-Fehler zu begehen oder festzustellen, dass es keinen Effekt gibt, wenn es tatsächlich einen gibt. Damit ist sie gleich 1 − \(\beta\), wobei \(\beta\) die Wahrscheinlichkeit ist, einen Fehler 2. Art zu begehen.

\[Power = 1 - \beta\]

Die statistische Macht \((1-\beta)\) wird grösser …

1. mit wachsender Grösse des wahren Unterschieds oder Effekts: Ein großer Unterschied zwischen zwei Teilpopulationen wird seltener übersehen als ein kleiner Unterschied.
   
2. mit kleiner werdender Merkmalsstreuung \(\sigma\): Dies kann z.B. durch die Unterteilung in homogenere Subpopulationen erreicht werden.
   
3. mit wachsendem Stichprobenumfang, da der Standardfehler \(SE\) kleiner wird.
   
4. mit grösser werdendem Signifikanzniveau \(\alpha\).

Wichtig für die statistische Macht bzw. Power ist auch die Art des statistischen Tests: Parametrische Tests wie zum Beispiel der \(t\)-Test haben, falls die Verteilungsannahme stimmt, bei gleichem Stichprobenumfang stets eine höhere Trennschärfe als nichtparametrische Tests.

Power-Analysen machen eine Aussage darüber, wie hoch die statistische Macht für ein Studiendesign ist. Sie werden entweder vor der eigentlichen Datenerhebung durchgeführt, um abzuschätzen wie viele Versuchspersonen für die Durchführung der Studie nötig sind, oder nach der eigentlichen Datenerhebung – dann in der Regel, wenn die Studie keine signifikanten Ergebnisse geliefert hat. In einem solchen Fall kann eine Power-Analyse Aufschluss darüber geben, wie viele Versuchsteilnehmer:innen noch nötig gewesen wären, damit der Effekt doch ein signifikantes Ergebnis geliefert hätte.

Beim Designen einer Studie, legt man gewöhnlicherweise das Powerniveau genauso fest, wie man es auch mit dem Signifikanzniveau macht. Oft wird eine statistische Power von 80 % gewählt, so dass ein echter Effekt in 20% der der Fälle nicht erkannt wird. Dies ist, wie oft in der Statistik, ein Kompromiss. Eine Erhöhung der Power auf beispielsweise 90 % würde auch mit einer Erhöhung des Stichprobenumfangs um etwa 30 % einhergehen, bei einer Erhöhung auf 95 % müsste man den Stichprobenumfang sogar um 60 % erhöhen, was in beiden Fällen die Kosten für die Studie erheblich erhöhen würde.

5.10 Einseitige und zweiseitige Hypothesentests

5.10.1 Einseitige Hypothesentests

Eine Studie der National Sleep Foundation hat herausgefunden, dass Schüler:innen im Durchschnitt 7 Stunden pro Nacht schlafen. Lehrer:innen an einer lokalen Schule mit über 2000 Schüler:innen waren überzeugt, dass diese im Durchschnitt länger als sieben Stunden schlafen. Ihre Fragestellung lautete: “Schlafen Schüler:innen an unserer Schule länger als 7 Stunden?”

Als erstes formulierten wir die mathematischen Hypothesen:

• \(H_0:~\mu = 7\), Schüler:innen an dieser Schule schlafen im Durchschnitt 7 Stunden (Nullwert).
  
• \(H_A:~\mu > 7\), Schüler:innen an dieser Schule schlafen im Durchschnitt länger als 7 Stunden.

Dies ist ein Beispiel für einen einseitigen Hypothesentest. Es interessiert bei dieser Fragestellung nicht, ob Schüler:innen weniger als 7 Stunden schlafen.

Die Lehrer:innen zogen eine Zufallsstichprobe von n = 110 Schüler:innen an ihrer Schule und fragten sie nach der üblichen Schlafdauer. Als Signifikanzniveau legten Sie \(\alpha=0.05\) fest. Die Erhebung ergab folgendes Resultat:

Tabelle 5.2: Kennzahlen zur Schlafdauer (h)

n	M	s	median
110	7.42	1.75	7.04

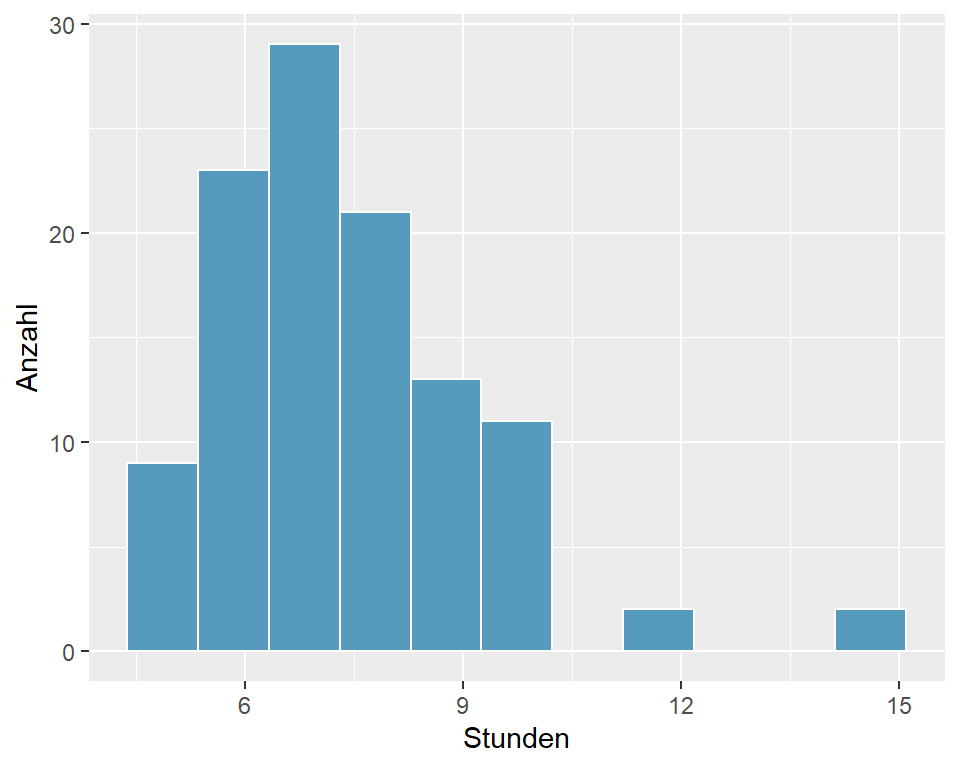
Abbildung 5.8: Schlafdauer (h) bei 110 Studierenden

Bevor das Normalmodell für den Stichprobenmittelwert bei der Berechnung des 95%-Vertrauensintervalls verwendet werden darf, muss überprüft werden, ob die Voraussetzungen erfüllt sind:

• Da es eine Zufallstichprobe von weniger als 10% der Studierenden ist, sind die Beobachtungen unabhängig.
  
• Die Stichprobengrösse ist genügend gross (n > 30).
  
• Die Daten sind auf Grund der beiden Ausreisser bei 12 und 15 Stunden linkssteil verteilt. Bei einer Stichprobengrösse von 110 darf dies jedoch vernachlässigt werden.

Da die Voraussetzungen weitgehend erfüllt sind, darf angenommen werden, dass die Populationsdaten normalverteilt sind.

## [1] 7.09 7.75

Prüfung mit dem 95%-Konfidenzintervall:

Das 95%-Vertrauensintervall für die durchschnittliche Schlafdauer der Schüler:innen beträgt [7.09; 7.75], d.h. wir können zu 95% darauf vertrauen, dass die durchschnittliche Schlafdauer 7.42 [7.09; 7.75] Stunden beträgt. Der Nullwert von 7 Stunden ist in diesem Vertrauensintervall nicht enthalten und wir verwerfen die \(H_0\) zugunsten der \(H_A\).

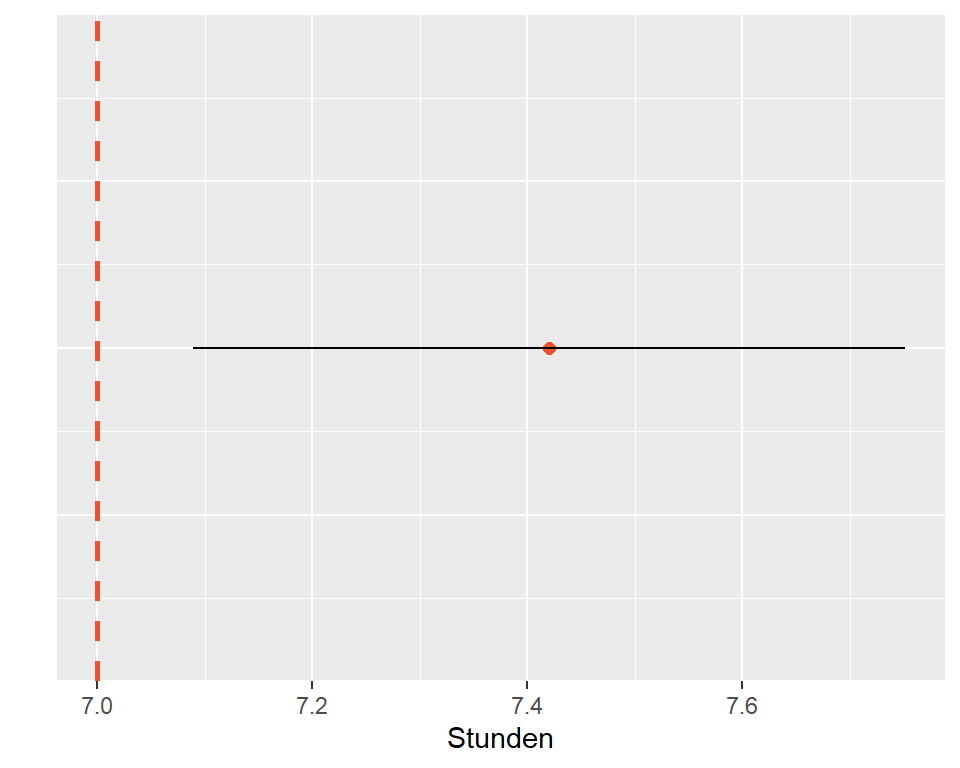
Abbildung 5.9: 95%-CI für die Schlafdauer der Schüler:innen, n = 110

Prüfung mit dem p-Wert:

Wir überprüfen, ob unsere Daten mit der \(H_0\) vereinbar sind. Wir zeichnen die Verteilung unter der Nullhypothese (kann man auch von Hand skizzieren, ist sehr zu empfehlen) und berechnen den \(z\)-Wert für den Mittelwert unserer Stichprobe.

\[z = \frac{\bar{x} - Nullwert}{SE} = \frac{7.42 - 7}{0.17} = 2.47\]

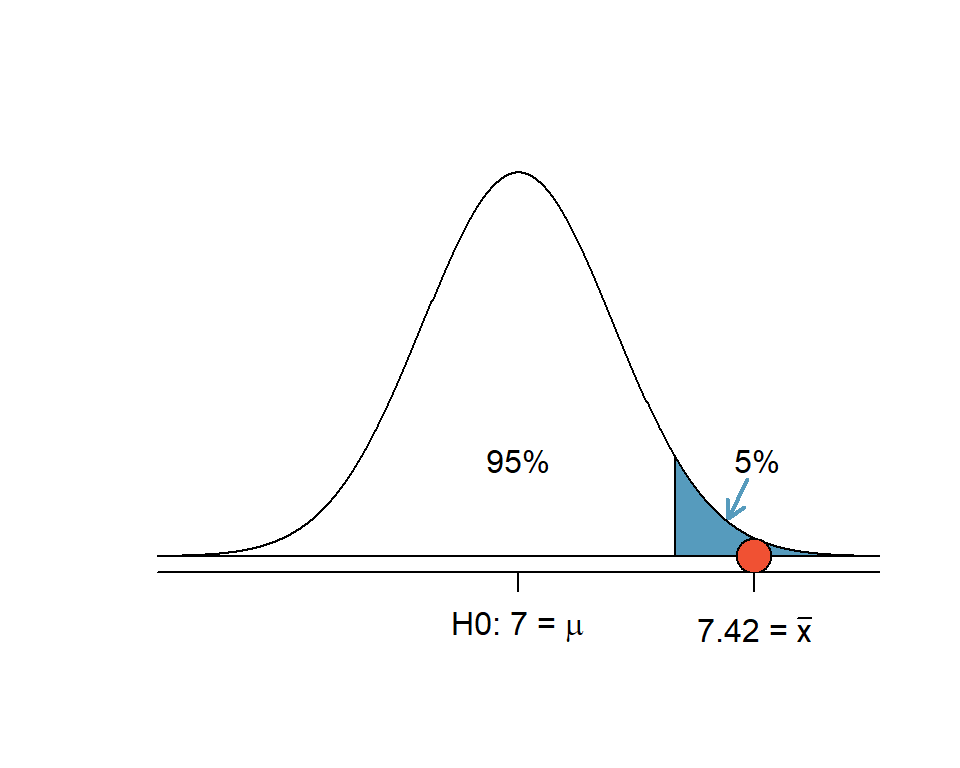
Abbildung 5.10: Einseitiger Hypothesentest: Der z-Wert 2.47 liegt im 5%-Verwerfungsbereich (blau)

In der Abbildung 5.10 ist der obere 5%-Verwerfungsbereich blau markiert. Wenn \(H_A\) einseitig \(\mu_1 > \mu_0\) formuliert ist und ein Wert in den oberen 5%-Bereich der Verteilung unter der Nullhypothese fällt, entscheiden wir für einen signifikanten Unterschied (auf der Entscheidungsgrundlage \(\alpha\) = 0.05).

Den \(p\)-Wert für \(z\) = 2.47 kann in einer \(z\)-Werte-Tabelle abgelesen werden oder - einfacher und genauer - mittels R berechnet werden.

### R-Code

pnorm(2.47)

## [1] 0.9932443

Die Fläche unter der Kurve links von unserem Stichprobenmittelwert ist 0.993. Somit ist die verbleibende Fläche 1 - 0.993 = 0.007.

### R-Code

1 - pnorm(2.47)

## [1] 0.006755653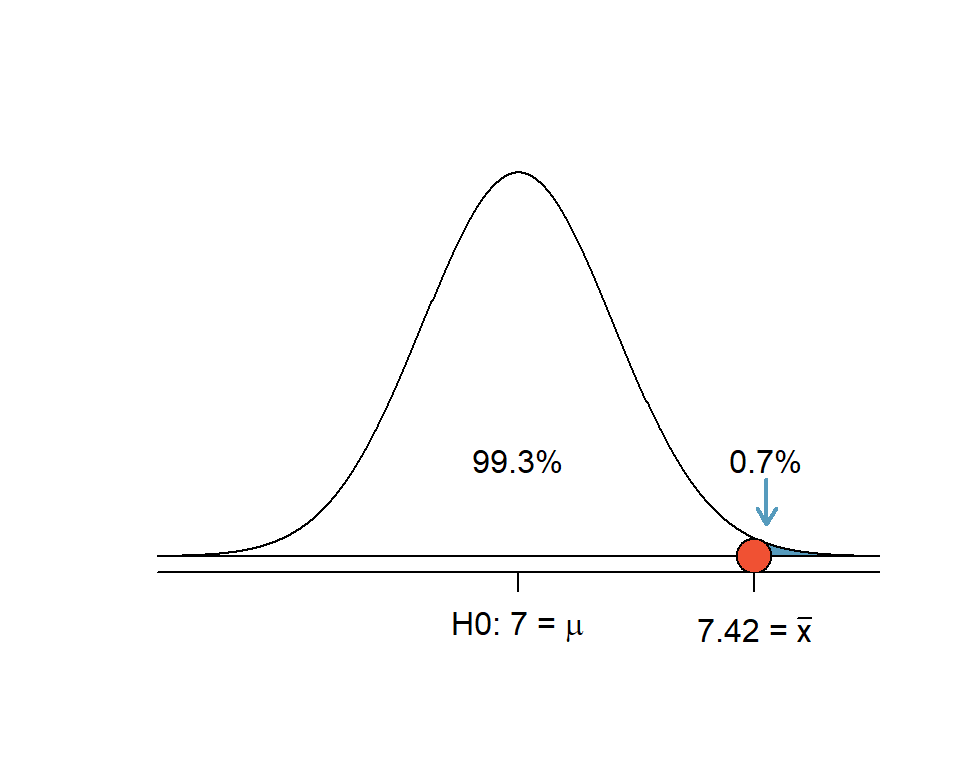

Abbildung 5.11: Einseitiger Hypothesentest: Die Fläche rechts vom z-Wert 2.47 (blau) beträgt 0.7% der Gesamtfläche unter der Kurve

Interpretation: Wenn die Nullhypothese wahr ist, dann liegt die Wahrscheinlichkeit für einen Stichprobenmittelwert von 7.42 oder mehr Stunden für eine Stichprobe von 110 Schülerinnen bei nur \(p\) = 0.007, bzw. 0.7%. Wenn die Nullhypothese wahr wäre, würden wir ein solches Ergebnis nur sehr selten antreffen. Weil der p-Wert kleiner als das festgelegte Signifikanzniveau \(\alpha = 0.05\) ist, verwerfen wir die Nullhypothese zugunsten der Alternativhypothese und kommen zum Schluss, dass die Schülerinnen an dieser Schule im Durchschnitt länger als 7 Stunden schlafen.

5.10.2 Zweiseitige Hypothesentests

In einseitigen Tests interessieren wir uns für den Bereich der Verteilung in der Richtung der Alternativhypothese. Im vorangehenden Beispiel war dies \(H_A: \mu > 7\). Somit liegt unser Verwerfungsbereich rechts vom Mittelwert unter \(H_0\). Die Alternativhypothese kann auch in die andere Richtung zeigen \(H_A: \mu < 7\), dann liegt unser Verwerfungsbereich links vom Mittelwert unter \(H_0\). Bei zweiseitigen Tests, interessieren uns beide Seiten der Verteilung und die Alternativhypothese ist symmetrisch formuliert \(H_A: \mu \neq 7\). Diese Formulierung lässt offen, ob der Populationsmittelwert gemäss unserer Stichproben nach oben oder nach unten abweicht. Die Frage lautet dann: “Unterscheidet sich unserer Mittelwert von dem der Population \(H_0\)?”, wobei der Mittelwert aus der Stichprobe sowohl kleiner als auch grösser als der Mittelwert unter \(H_0\) sein kann.

Wie wir gesehen haben, hat die National Sleep Foundation festgestellt, dass Schülerinnen im Durchschnitt 7 Stunden schlafen. Eine andere Forschungsgruppe wollte wissen, ob sich die Schlafdauer der Schülerinnen an ihrer Schule von dieser Norm unterscheidet. Sie formulierten die Hypothesen:

\(H_0: \mu = 7\), die durchschnittliche Schlafdauer beträgt 7 Stunden.
\(H_A: \mu \neq 7\), die durchschnittliche Schlafdauer unterscheidet sich von 7 Stunden.

Diese zweite Gruppe hat randomisiert 122 Schülerinnen zu ihrer Schlafdauer befragt. Das Ergebnis war, dass die Schülerinnen an dieser Schule im Durchschnitt \(\bar{x}=6.83\) Stunden schlafen (s = 1.8 Stunden). Haben wir damit Evidenz gegen die Nullhypothese (\(\alpha = 0.05\))?

1. Prüfen der Voraussetzungen: (1) Eine Zufallsstichprobe von weniger als 10% der Schülerinnen bedeutet, dass die Beobachtungen unabhängig sind. (2) Der Stichprobenumfang ist grösser als 30. (3) Aufgrund der Überlegungen im letzten Beispiel können wir davon ausgehen, dass der Stichprobenumfang ausreichen gross ist, damit die Stichprobenmittelwerte normal verteilt sind.

2. Den Standardfehler SE berechnen:

### R-Code

n <- 122
m <- 6.83
s <- 1.8
SE <- s/sqrt(n)
SE

## [1] 0.1629643

Der Standardfehler ist \(SE\) = 0.163.

3. Eine Skizze erstellen:

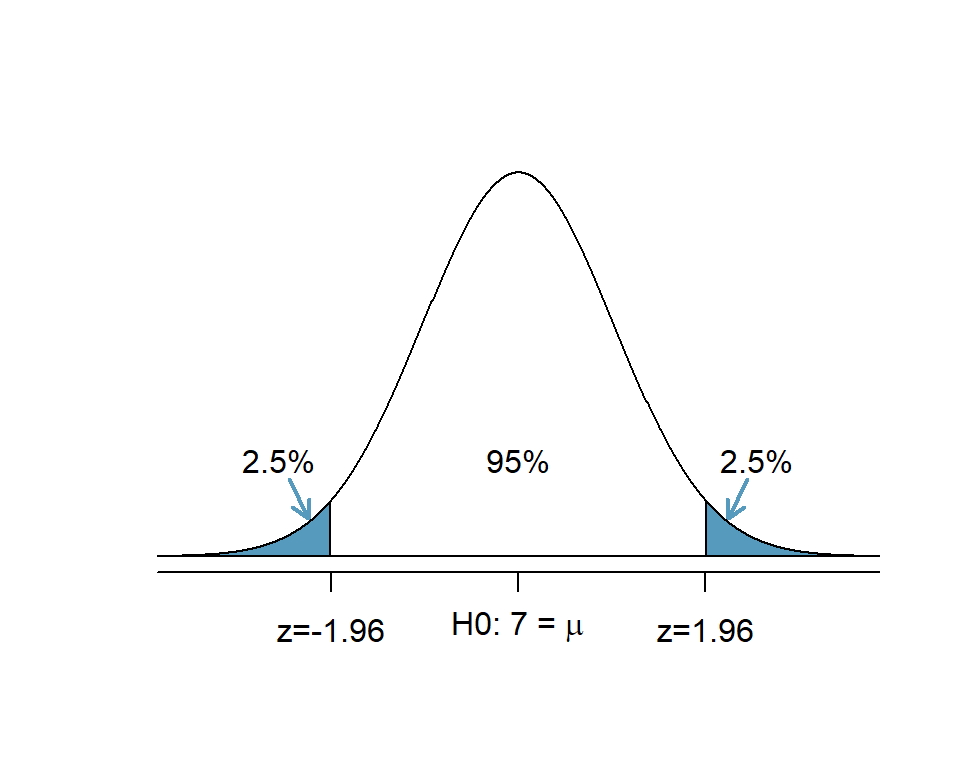
Abbildung 5.12: Zweiseitiger Hypothesentest: Der 5%-Verwerfungsbereich (blau) verteilt sich auf die beiden Enden der Verteilung

Da wir unsere Alternativhypothese zweiseitig formuliert haben, wird der Verwerfungsbereich auf 2.5% am unteren und 2.5% am oberen Ende der Verteilung aufgeteilt. Die Grenze zu den Verwerfungsbereichen liegt bei z=-1.96 und z=+1.96.

4. Berechnung des \(z\)-Werts:

\[z = \frac{6.83 - 7}{0.16} = -1.06\]

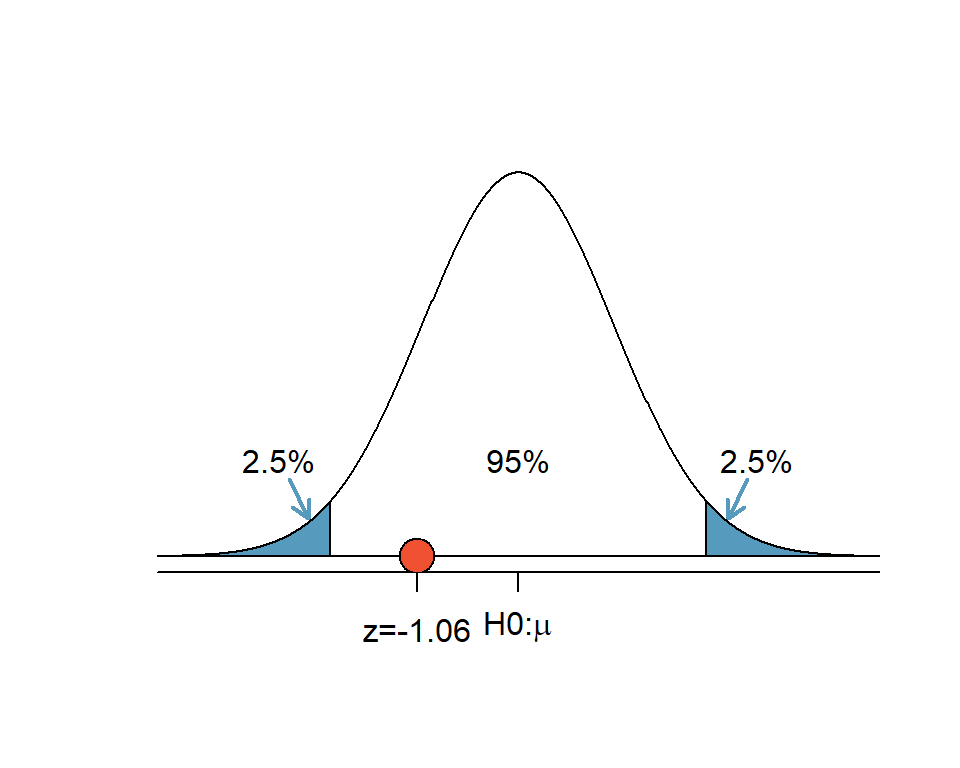
Abbildung 5.13: Zweiseitiger Hypothesentest: Der z-Wert für den Stichprobenmittelwert liegt im Nichtverwerfungsbereich

Der \(p\)-Wert für die linke Fläche bei \(z\) = -1.06 ist 0.145. Weil das Normalmodell symmetrisch ist, muss die rechte Hälfte die selbe Fläche haben wie die linke Fläche. Der \(p\)-Wert wird daher für die Summe beider Flächen berechnet:

### R-Code

linke_flaeche <- pnorm(-1.06)     # Fläche <= -1.06
rechte_flaeche <- 1-pnorm(1.06)   # Fläche >= 1.06

p <- linke_flaeche + rechte_flaeche
p

## [1] 0.2891446

Ein p-Wert von 0.29 ist relativ gross (grösser als \(\alpha = 0.05)\) und wir wir haben keine Evidenz gegen \(H_0\). Das heisst, wenn \(H_0\) wahr ist, ist es nicht aussergewöhnlich, wenn man einen Mittelwert erhält, der sich so wenig von 7 Stunden unterscheidet. Die Ursache für die geringe Abweichung des Mittelwerts von 7 Stunden kann alleine auf der Stichprobenvariation beruhen.

5.10.3 Einseitige vs. zweiseitige Hypothesentests

Wir bevorzugen grundsätzlich die Verwendung von zweiseitigen Arbeitshypothesen. Warum? Einseitige Hypothesentests verdoppeln das Risiko, einen Fehler 1. Art zu begehen. Es ist unlautere wissenschaftliche Praxis, wenn nach der Datenerhebung eine zweiseitige Alternativhypothese zu einer einseitigen Alternativhypothese geändert wird, mit der Absicht, statistisch signifikante Effekte zu erhalten, weil solche eher publiziert werden als nicht signifikante Resultate. Deshalb müssen die Hypothesen bei der Registrierung von Studien immer vor der Datenerhebung deklariert werden.

5.11 Hypothesentests Schritt für Schritt

1. Notiere die Hypothesen in Umgangssprache. Übersetze sie dann in mathematische Notation.
   
2. Identifiziere die korrekte Prüfgrösse für die Fragestellung.
   
3. Prüfe die Voraussetzungen für die Durchführung der Tests (Unabhängigkeit, \(n\) > 30, Normalverteilung)
   
4. Berechne die Kennzahlen und den Standardfehler. Erstelle eine Skizze für die Verteilung unter \(H_0\). Markiere die Verwerfungsbereiche.
   
5. Berechne die Teststatistik (z.B. den \(z\)-Wert) und den zugehörigen p-Wert.
   
6. Berechne das 95%-Konfidenzintervall für den Populationsparameter.
7. Schreibe eine Schlussfolgerung in einer Sprache, sie auch für Nichtstatistiker:innen verständlich ist. Vermeide es, nur einen \(p\)-Wert ohne Kennzahlen für Punktschätzer und 95%-Konfidenzintervall anzugeben.

5.12 Statistische Signifikanz versus praktische Relevanz

Eine Konsequenz des Wurzel-n-Gesetzes ist es, dass es bloss eine Frage des Stichprobenumfangs ist, ob auch kleine Effekte statistisch signifikant werden. Die Aussage, dass ein Ergebnis statistisch signifikant ist, bedeutet nicht, dass es auch von praktischer Bedeutung ist. In den Gesundheitsberufen müssen wir einen Effekt immer in Bezug zur MCID (minimal clinical important difference) setzen, sofern dieser bekannt ist.

Beispiel: In einer Studie wird der Effekt einer neuen Behandlung auf das subjektive Schmerzempfinden bei Rückenschmerzpatienten gemessen. Die Intervention ist vielversprechend aber auch wesentlich teurer, als die bisherige Standardbehandlung. Das Studiendesign entspricht einer randomisierten kontrollierten Studie (RCT). Die Kontrollgruppe erhält die bisherige Standardbehandlung, die Interventionsgruppe erhält die neue Behandlung. Gemessen wird der Effekt der Behandlungen auf die subjektiven Schmerzen auf einer VAS-Skala von 0 bis 10. Die Studie kommt zum Schluss, dass die Intervention im Durchschnitt eine signifikante Verbesserung bei der Interventionsgruppe gegenüber der Kontrollgruppe von VAS -1.5 [-1.7 -1.3] mit p < 0.05 ergibt. Auf Grund dieser Ergebnisse stellt sich die Frage, ob die alte Behandlung aufgegeben und durch die neue ersetzt werden muss. Um diese Frage zu beantworten, müssen wir wissen, wie gross der Effekt einer Behandlung sein muss, damit die Patientinnen subjektiv eine Verbesserung ihrer Schmerzen wahrnehmen. Eine Suche in der Literatur ergibt, dass die MCID (minimal clinical important difference) bei einer Reduktion der VAS um -2 liegt. Mit anderen Worten: Die neue Intervention mag zwar eine statistisch signifikante Verbesserung von VAS -1.5 bewirken, für die Patient:innen ist das aber nicht von Bedeutung (nicht klinisch relevant), weil sie subjektiv erst ab einer Reduktion der VAS um -2 einen Effekt und damit eine Verbesserung ihrer Lebensqualität wahrnehmen. Vor allem in Anbetracht der zusätzlichen Kosten der neuen Intervention, besteht keine Evidenz dafür, dass diese die bisherige Standardtherapie ersetzen sollte. (Ostelo and Vet 2005)

References

Ostelo, R. W., and H. C. de Vet. 2005. “Clinically Important Outcomes in Low Back Pain.” Best Practice & Research. Clinical Rheumatology 19: 593–607. https://doi.org/10.1016/j.berh.2005.03.003.